
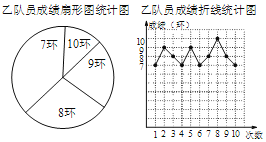
【题目】某射击队准备从甲、乙两名队员中选取一名队员代表该队参加比赛,特为甲、乙两名队员单行了一次选拔赛,要求这两名队员各射击10次,比赛结束后,根据比赛成绩情况,将甲,乙两名队员的比赛成绩制成了如下的统计图(表):
甲队员的成绩统计表:
成绩(单位:环) | 7 | 8 | 9 | 10 |
次数(单位:次) | 5 | 1 | 3 | 1 |
(1)在乙队员成绩扇形统计图中,求“8环”所在扇形的圆心角的度数;
(2)经过整理,得到的分析数据如表:
队员 | 平均数 | 中位数 | 众数 | 方差 |
甲 | 8 | 7.5 | 7 | c |
乙 | a | 8 | b | 1 |
求表中的a、b、c的值(3)根据甲、乙两名队员的成绩情况,该射击队准备选派乙参加比赛,请你写出一条射击队选派乙的理由.
【答案】(1)108°;(2)a的值为8,b的值为8,c的值为1.2;(3)见解析.
【解析】
(1)用360°乘以对应次数所占比例即可;
(2)根据平均数,众数和方差的定义计算即可;
(3)可以从中位数和方差的角度来解答,答案不唯一.
解:(1)根据乙队员折线图可知,8环的次数是3次,一共是10次成绩,所以8环次数的占比是![]() ,
,
所以“8环”所在扇形的圆心角的度数:360°×![]() =108°,
=108°,
答:乙队员成绩扇形统计图中,“8环”所在扇形的圆心角的度数为108°.
(2)由折线图可知10次成绩分别是7,9,8,7,9,7,8,10,8,7,所以平均成绩是
a=![]() =8,
=8,
乙队员10次成绩从小到大排列为:7,7,7,7,8,8,8,9,9,10,处在第5、6位的两个数都是8环,因此众数是8环,
c=![]() [(7﹣8)2×5+(8﹣8)2+(9﹣8)2×3+(10﹣8)2]
[(7﹣8)2×5+(8﹣8)2+(9﹣8)2×3+(10﹣8)2]
=1.2,
答:a的值为8,b的值为8,c的值为1.2.
(3)选择乙队,理由为:乙的方差小,比较稳定,中位数和众数都是8环,均比甲队员高(答案不唯一).


科目:初中数学 来源: 题型:
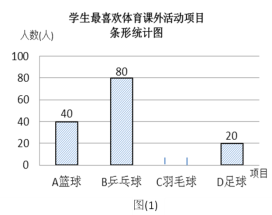
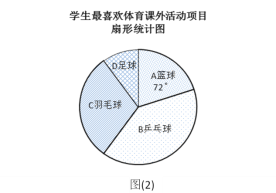
【题目】某学校为了丰富学生课余生活,决定开设以下体育课外活动项目:A篮球;B乒乓球;C羽毛球;D足球,为了解学生最喜欢哪一种活动项目,随机抽取了部分学生进行调查,并将调查结果绘制成了两幅不完整的统计图,请回答下列问题:
(1)这次被调查的学生共有__________人;
(2)请你将条形统计图(1)补充完整;
(3)在平时的乒乓球项目训练中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中任选两名参加乒乓球比赛,求恰好选中甲、乙两位同学的概率(用树状图或列表法解答)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一面靠墙(墙的最大可用长度为8 m)的空地上用长为24 m的篱笆围成中间隔有二道篱笆的长方形花圃.设花圃的宽AB为x m,面积为S m2.
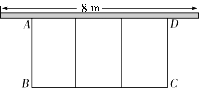
(1)求S关于x的函数关系式及自变量的取值范围;
(2)求所围成花圃的最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个二次函数图像上部分点的横坐标![]() ,纵坐标
,纵坐标![]() 的对应值如下表:
的对应值如下表:
| … | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | … |
| … |
| 0 |
| 2 |
| 0 |
| -6 |
| … |
(1)![]() 的值为______;
的值为______;
(2)在给定的直角坐标系中,画出这个函数的图像;
(3)当![]() 时,求
时,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若整数a既使关于x的分式方程![]() ﹣
﹣![]() =1的解为非负数,又使不等式组
=1的解为非负数,又使不等式组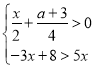 有解,且至多有5个整数解,则满足条件的a的和为( )
有解,且至多有5个整数解,则满足条件的a的和为( )
A.﹣5B.﹣3C.3D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,点C为圆上一点,∠BAC=20°,将劣弧![]() 沿弦AC所在的直线翻折,交AB于点D,则弧
沿弦AC所在的直线翻折,交AB于点D,则弧![]() 的度数等于( )
的度数等于( )
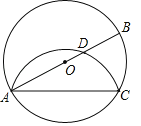
A.40°B.50C.80°D.100
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形网格中,建立如图所示的平面直角坐标系xOy,ΔABC的三个顶点都在格点上,点A的坐标(4,4),请解答下列问题:
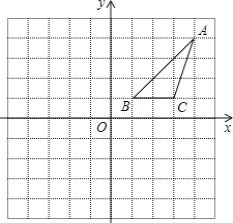
(1)画出ΔABC关于y轴对称的ΔA1B1C1,并写出点A1,B1,C1的坐标;
(2)将ΔABC绕点C逆时针旋转90°,画出旋转后的ΔA2B2C,并写出点A2,B2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017江西省)如图1,研究发现,科学使用电脑时,望向荧光屏幕画面的“视线角”α约为20°,而当手指接触键盘时,肘部形成的“手肘角”β约为100°.图2是其侧面简化示意图,其中视线AB水平,且与屏幕BC垂直.
(1)若屏幕上下宽BC=20cm,科学使用电脑时,求眼睛与屏幕的最短距离AB的长;
(2)若肩膀到水平地面的距离DG=100cm,上臂DE=30cm,下臂EF水平放置在键盘上,其到地面的距离FH=72cm.请判断此时β是否符合科学要求的100°?
(参考数据:sin69°≈![]() ,cos21°≈
,cos21°≈![]() ,tan20°≈
,tan20°≈![]() ,tan43°≈
,tan43°≈![]() ,所有结果精确到个位)
,所有结果精确到个位)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com