
【题目】如图,一次函数![]() 与反比例函数
与反比例函数![]()
![]() 的图象相交于点
的图象相交于点![]() 和
和![]() .
.

(1)求一次函数和反比例函数的解析式;
(2)若定义横、纵坐标均为整数的点叫做好点,则图中阴影部分区域内(不含边界)好点的个数为________;
(3)请根据图象直接写出不等式![]() 的解集.
的解集.
【答案】(1)反比例函数的解析式为![]() ,一次函数的解析式为
,一次函数的解析式为![]() ;(2)7个;(3)
;(2)7个;(3)![]() 或
或![]() .
.
【解析】
(1)把A(2,3)代入![]() 可求得k=6,把B(m,-1)代入
可求得k=6,把B(m,-1)代入![]() 得m=-6,把A(2,3),B(-6,-1)代入y=ax+b即可求出a,b的值;
得m=-6,把A(2,3),B(-6,-1)代入y=ax+b即可求出a,b的值;
(2)求出直线![]() 与y轴的交点坐标结合直线与双曲线在第一象限内的交点坐标即可确定好点的个数;
与y轴的交点坐标结合直线与双曲线在第一象限内的交点坐标即可确定好点的个数;
(3)根据图象确定直线在双曲线下方时,确定x的取值范围即可.
(1)将点![]() 代入
代入![]() 得,
得,![]() ,
,
∴反比例函数的解析式为:![]() .
.
将点![]() 代入
代入![]() 得,
得,![]() .
.
将点![]() ,
,![]() 代入
代入![]() 得,
得,
![]()
解得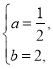
∴一次函数的解析式为:![]() .
.
(2)令x=0,得y=2,所以直线![]() 与y轴的交点坐标为(0,2)
与y轴的交点坐标为(0,2)
故阴影部分内(不含边界)整点坐标有(1,1),(1,2),(1,3),(2,1),(2,2),(4,1),(5,1)共7个;
(3)∵A(2,3),B(-6,1)且![]()
由图象可得x的取值范围是:![]() 或
或![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在二次函数y=ax2+bx+c(a≠0)的图象中,小明同学观察得出了下面几条信息:①b2﹣4ac>0;②abc<0;③![]() ;④b2=4a(c﹣1);⑤关于x的一元二次方程ax2+bx+c=3无实数根,共中信息错误的个数为( )
;④b2=4a(c﹣1);⑤关于x的一元二次方程ax2+bx+c=3无实数根,共中信息错误的个数为( )
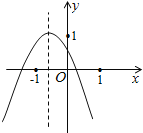
A.4B.3C.2D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣x2+2x+3,截取该函数图象在0≤x≤4间的部分记为图象G,设经过点(0,t)且平行于x轴的直线为l,将图象G在直线l下方的部分沿直线l翻折,图象G在直线上方的部分不变,得到一个新函数的图象M,若函数M的最大值与最小值的差不大于5,则t的取值范围是( )
A.﹣1≤t≤0B.﹣1≤t![]() C.
C.![]() D.t≤﹣1或t≥0
D.t≤﹣1或t≥0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】李明准备进行如下操作实验,把一根长40 cm的铁丝剪成两段,并把每段首尾相连各围成一个正方形.
(1)要使这两个正方形的面积之和等于58 cm2,李明应该怎么剪这根铁丝?
(2)李明认为这两个正方形的面积之和不可能等于48 cm2,你认为他的说法正确吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
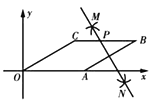
【题目】如图,在菱形![]() 中,
中,![]() ,
,![]() ,以
,以![]() 为坐标原点,以
为坐标原点,以![]() 所在的直线为
所在的直线为![]() 轴建立平面直角坐标系,如图.按以下步骤作图:①分别以点
轴建立平面直角坐标系,如图.按以下步骤作图:①分别以点![]() ,
,![]() 为圆心,以大于
为圆心,以大于![]() 的长为半径作弧,两弧相交于点
的长为半径作弧,两弧相交于点![]() ,
,![]() ;②作直线
;②作直线![]() 交
交![]() 于点
于点![]() .则点
.则点![]() 的坐标为( )
的坐标为( )
A.![]() B.
B.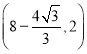 C.
C.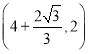 D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,若O为BC边的中点,则必有:AB2+AC2=2AO2+2BO2成立.依据以上结论,解决如下问题:如图,在矩形DEFG中,已知DE=4,EF=3,点P在以DE为直径的半圆上运动,则PF2+PG2的最小值为( )

A. ![]() B.
B. ![]() C. 34 D. 10
C. 34 D. 10
查看答案和解析>>
科目:初中数学 来源: 题型:
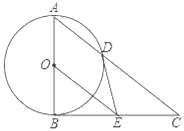
【题目】如图,AB为⊙O直径,BC为⊙O切线,连接A、C两点,交⊙O于点D,BE=CE,连接DE,OE.
(1)判断DE与⊙O的位置关系,并说明理由;
(2)求证:BC2=CD2OE;
(3)若cos∠BAD=![]() ,BE=6,求OE的长.
,BE=6,求OE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,D、E分别是斜边AB、直角边BC上的点,把
,D、E分别是斜边AB、直角边BC上的点,把![]() 沿着直线DE折叠.
沿着直线DE折叠.

![]() 如图1,当折叠后点B和点A重合时,用直尺和圆规作出直线DE;
如图1,当折叠后点B和点A重合时,用直尺和圆规作出直线DE;![]() 不写作法和证明,保留作图痕迹
不写作法和证明,保留作图痕迹![]()
![]() 如图2,当折叠后点B落在AC边上点P处,且四边形PEBD是菱形时,求折痕DE的长.
如图2,当折叠后点B落在AC边上点P处,且四边形PEBD是菱形时,求折痕DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
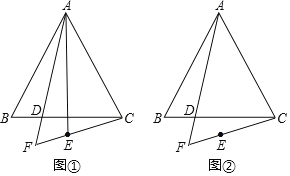
【题目】在等边△ABC中,点D是边BC上一点.作射线AD,点B关于射线AD的对称点为点E.连接CE并延长,交射线AD于点F.
(1)如图①,连接AE,
①AE与AC的数量关系是 ;
②设∠BAF=a,用a表示∠BCF的大小;
(2)如图②,用等式表示线段AF,CF,EF之间的数量关系,并证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com