
【题目】综合与实践
(1)(探索发现)在![]() 中.
中. ![]() ,
,![]() ,点
,点![]() 为直线
为直线![]() 上一动点(点
上一动点(点![]() 不与点
不与点![]() ,
,![]() 重合),过点
重合),过点![]() 作
作![]() 交直线
交直线![]() 于点
于点![]() ,将
,将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到
得到![]() ,连接
,连接![]() .
.
如图(1),当点![]() 在线段
在线段![]() 上,且
上,且![]() 时,试猜想:
时,试猜想:
①![]() 与
与![]() 之间的数量关系:______;
之间的数量关系:______;
②![]() ______.
______.
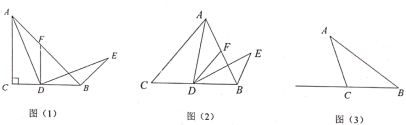
(2)(拓展探究)
如图(2),当点![]() 在线段
在线段![]() 上,且
上,且![]() 时,判断
时,判断![]() 与
与![]() 之间的数量关系及
之间的数量关系及![]() 的度数,请说明理由.
的度数,请说明理由.
(3)(解决问题)
如图(3),在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 在射线
在射线![]() 上,将
上,将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到
得到![]() ,连接
,连接![]() .当
.当![]() 时,直接写出
时,直接写出![]() 的长.
的长.
【答案】(1)①![]() ;②
;②![]() ;(2)
;(2)![]() ,
,![]() .理由见解析;(3)
.理由见解析;(3)![]() 的长为1或2.
的长为1或2.
【解析】
(1)由“SAS”△ADF≌△EDB,可得AF=BE,再利用“8字型”字母∠OBE=∠ADO=90°即可解决问题;
(2)结论:AF=BF,∠ABE=a.由“SAS”△ADF≌△EDB,即可解决问题;
(3)分当点D在线段BC上和当点D在BC的延长线上两种情形讨论,利用平行线分线段成比例可求解.
解:
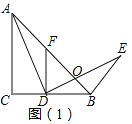
(1)如图1中,设AB交DE于O.
∵∠ACB=90°,AC=BC,
∴∠ABC=45°,
∵DF∥AC,
∴∠FDB=∠C=90°,
∴∠DFB=∠DBF=45°,
∴DF=DB,
∵∠ADE=∠FDB=90°,
∴∠ADF=∠EDB,且DA=DE,DF=DB
∴△ADF≌△EDB(SAS),
∴AF=BE,∠DAF=∠E,
∵∠AOD=∠EOB,
∴∠ABE=∠ADO=90°
故答案为AF=BE,90°.
(2)![]() ,
,![]() .
.
理由:∵![]() ,
,
∴![]() ,
,![]() .
.
∵![]() ,
,
∴![]() .∴
.∴![]() .
.
∴![]()
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() .
.
又∵![]() ,
,
∴![]() .
.
∴![]() ,
,![]() .
.
∴![]() ,
,![]() ,
,
∴![]() .
.
(3)1或2.
解:当点![]() 在线段
在线段![]() 上时,过点
上时,过点![]() 作
作![]() 交直线
交直线![]() 于点
于点![]() ,如图(1).
,如图(1).
∵![]() ,∴
,∴![]() .
.
∵![]() ,∴
,∴![]() .
.
∵![]() ,∴
,∴![]() ,
,![]() .
.
∵![]() ,
,![]() ,
,
∴![]() .
.
∵![]() ,∴
,∴![]() .∴
.∴![]() .∴
.∴![]() .
.
又![]() ,∴
,∴![]() ,
,![]() .
.
当点![]() 在线段
在线段![]() 的延长线上时,过点
的延长线上时,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,如图(2).
,如图(2).
∵![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() .
.
同理可得![]() .
.
综上可得,![]() 的长为1或2.
的长为1或2.


 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:初中数学 来源: 题型:
【题目】定义:如图1,对于直线![]() 同侧的
同侧的![]() 、
、![]() 两点,若在
两点,若在![]() 上的点
上的点![]() 满足
满足![]() ,则称
,则称![]() 为
为![]() 、
、![]() 两点在
两点在![]() 上的反射点,
上的反射点,![]() 与
与![]() 的和称为
的和称为![]() 、
、![]() 两点的反射距离.
两点的反射距离.

(1)如图2,在边长为2的正方形![]() 中,
中,![]() 为
为![]() 的中点,
的中点,![]() 为
为![]() 、
、![]() 两点在直线
两点在直线![]() 上的反射点,求
上的反射点,求![]() 、
、![]() 两点的反射距离;
两点的反射距离;
(2)如图3,![]() 内接于
内接于![]() ,直径
,直径![]() 为4,
为4,![]() ,点
,点![]() 为劣弧
为劣弧![]() 上一动点,点
上一动点,点![]() 为
为![]() 、
、![]() 两点在
两点在![]() 上的反射点,当
上的反射点,当![]() 、
、![]() 两点的反射距离最大时,求劣弧
两点的反射距离最大时,求劣弧![]() 的长;
的长;
(3)如图4,在平面直角坐标系中,抛物线![]() 与
与![]() 轴正半轴交于点
轴正半轴交于点![]() ,顶点为
,顶点为![]() ,若点
,若点![]() 为点
为点![]() 、
、![]() 在
在![]() 上的反射点,同时点
上的反射点,同时点![]() 为点
为点![]() 、
、![]() 在
在![]() 上的反射点.
上的反射点.
①请判断线段![]() 和
和![]() 的位置关系,并给出证明;
的位置关系,并给出证明;
②求![]() 、
、![]() 两点的反射距离与
两点的反射距离与![]() 、
、![]() 两点的反射距离的比值.
两点的反射距离的比值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“绿水青山就是金山银山”,为保护生态环境,A,B两村准备各自清理所属区域养鱼网箱和捕鱼网箱,每村参加清理人数及总开支如下表:
村庄 | 清理养鱼网箱人数/人 | 清理捕鱼网箱人数/人 | 总支出/元 |
A | 15 | 9 | 57000 |
B | 10 | 16 | 68000 |
(1)若两村清理同类渔具的人均支出费用一样,求清理养鱼网箱和捕鱼网箱的人均支出费用各是多少元;
(2)在人均支出费用不变的情况下,为节约开支,两村准备抽调40人共同清理养鱼网箱和捕鱼网箱,要使总支出不超过102000元,且清理养鱼网箱人数小于清理捕鱼网箱人数,则有哪几种分配清理人员方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
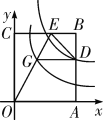
【题目】矩形OABC有两边在坐标轴的正半轴上,OA=4,OC=6,如图,双曲线y=![]() 与边AB交于点D,过点D作DG∥OA,交双曲线y=
与边AB交于点D,过点D作DG∥OA,交双曲线y=![]() (k>0)于点G,连接OG并延长交CB于点E,若∠EGD=∠EDG,则k的值为______.
(k>0)于点G,连接OG并延长交CB于点E,若∠EGD=∠EDG,则k的值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点坐标是A(0,﹣2),B(6,﹣4),C(2,﹣6).
(1)请画出与△ABC关于x轴对称的△A1B1C1.
(2)以点O为位似中心,将△ABC缩小为原来的![]() ,得到△A2B2C2,请在y轴左侧画出△A2B2C2.
,得到△A2B2C2,请在y轴左侧画出△A2B2C2.
(3)在y轴上存在点P,使得△OB2P的面积为6,请直接写出满足条件的点P的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com