
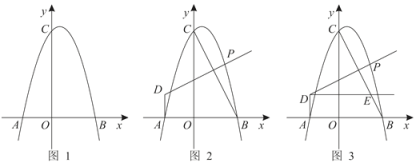
【题目】已知:如图,抛物线![]() 交x轴于A(-2,0),B(3,0)两点,交y轴于点C(0,6).
交x轴于A(-2,0),B(3,0)两点,交y轴于点C(0,6).
(1)写出a,b,c的值;
(2)连接BC,点P为第一象限抛物线上一点,过点A作AD⊥x轴,过点P作PD⊥BC于交直线AD于点D,设点P的横坐标为t,AD长为h.
①求h与t的函数关系式和h的最大值(请求出自变量t的取值范围);
②过第二象限点D作DE∥AB交BC于点E,若DP=CE,时,求点P的坐标.
【答案】(1)a=-1,b=1,c=6;(2)①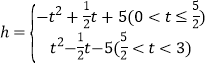 ,当
,当![]() 时,h有最大值为
时,h有最大值为![]() ,当
,当![]() <t<3时,
<t<3时,![]() 无最大值,②符合条件的点P的坐标为(2,4).
无最大值,②符合条件的点P的坐标为(2,4).
【解析】
(1)根据待定系数法求解;(2)①如图,过点P作PG⊥x于点G,过点D作DK∥x轴交PG于点K,根据三角函数值和矩形性质得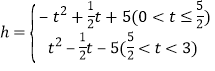 ,再求最值;②如图,过点P作PH⊥AD交AD的延长线于点H,根据全等三角形判定和性质,△PHD≌△CNE(AAS),PH=CN=OC-ON,根据矩形性质,t+2=
,再求最值;②如图,过点P作PH⊥AD交AD的延长线于点H,根据全等三角形判定和性质,△PHD≌△CNE(AAS),PH=CN=OC-ON,根据矩形性质,t+2=![]() ,解得
,解得![]() ,
,![]() (舍去),把t=2代入抛物线
(舍去),把t=2代入抛物线![]() ,可求点P(2,4).当点D在第三象限时,不存在点P满足DP=CE.故符合条件的点P的坐标为(2,4).
,可求点P(2,4).当点D在第三象限时,不存在点P满足DP=CE.故符合条件的点P的坐标为(2,4).
(1)根据题意得
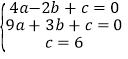
所以,a=-1,b=1,c=6;
(2)①如图,过点P作PG⊥x于点G,过点D作DK∥x轴交PG于点K,
∵PD⊥BC,DK⊥y轴,∠BCO=∠PDK,OB=3,OC=6,
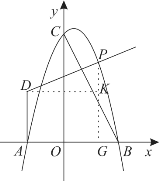
∴tan∠BCO=tan∠PDK=![]() ,DK=t+2,PK=
,DK=t+2,PK=![]() DK=
DK=![]() ,
,
∵DK∥AB,AD⊥AB,∴四边形ADKG为矩形,
∴AD=KG,
h=AD=KG=|PG-PK|=![]()
令![]() ,
,![]() ,
,![]() ,
,![]() (不合题意,舍去)
(不合题意,舍去)
∴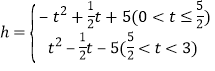
当0<t≤![]() 时,
时,![]()
![]()
∴当![]() 时,h有最大值为
时,h有最大值为![]()
当![]() <t<3时,
<t<3时,![]() 无最大值.
无最大值.
②如图,过点P作PH⊥AD交AD的延长线于点H,
∵PD⊥BC,∴∠PHD=∠ECE=90°-∠CMH
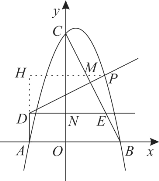
在△PHD与△CNE中,
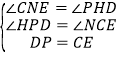 ,
,
∴△PHD≌△CNE(AAS),
∴PH=CN=OC-ON,
∵四边形ADNO为矩形,
∴CN=![]() =
=![]() ,PH=t+2,
,PH=t+2,
∴t+2=![]() ,
,
解得![]() ,
,![]() (舍去),
(舍去),
把t=2代入抛物线![]() ,∴点P(2,4).
,∴点P(2,4).
当点D在第三象限时,不存在点P满足DP=CE.
∴符合条件的点P的坐标为(2,4).


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:初中数学 来源: 题型:
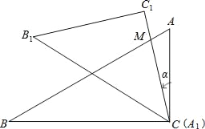
【题目】如图,是一副学生用的三角板,在△ABC 中,∠C=90°,∠A=60°,∠B=30°;在△A1B1C1中,∠C1=90°,∠B1A1 C1=45°,∠B1=45°,且A1B1=CB.若将边A1C1与边CA重合,其中点A1与点C重合.将三角板A1B1C1绕点C(A1)按逆时针方向旋转,旋转过的角为α,旋转过程中边A1C1与边AB的交点为M,设AC=a.
(1)计算A1C1的长;
(2)当α=30°时,证明:B1C1∥AB;
(3)若a=![]() ,当α=45°时,计算两个三角板重叠部分图形的面积;
,当α=45°时,计算两个三角板重叠部分图形的面积;
(4)当α=60°时,用含a的代数式表示两个三角板重叠部分图形的面积.
(参考数据:sin15°=![]() ,cos15°=
,cos15°=![]() ,tan15°=2﹣
,tan15°=2﹣![]() ,sin75°=
,sin75°=![]() ,cos75°=
,cos75°=![]() ,tan75°=2+
,tan75°=2+![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
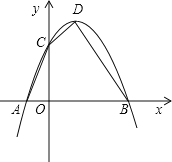
【题目】已知:如图,抛物线y=ax2-2ax+c(a≠0)与y轴交于点C(0,3),与x轴交于A、B两点,点A的坐标为(-1,0).
(1)求抛物线的解析式及顶点D的坐标;
(2)设点P是在第一象限内抛物线上的一个动点,求使与四边形ACDB面积相等的四边形ACPB的点P的坐标;
(3)求△APD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
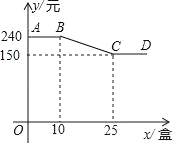
【题目】中秋节前夕,某公司的李会计受公司委派去超市购买若干盒美心月饼,超市给出了该种月饼不同购买数量的价格优惠,如图,折线ABCD表示购买这种月饼每盒的价格y(元)与盒数x(盒)之间的函数关系.
(1)当购买这种月饼盒数不超过10盒时,一盒月饼的价格为 元;
(2)求出当10<x<25时,y与x之间的函数关系式;
(3)当时李会计支付了3600元购买这种月饼,那么李会计买了多少盒这种月饼?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,

(1)请用直尺和圆规按下列步骤作图(保留作图痕迹),①作![]() 的平分线,交斜边AB于点D;②过点D作AC的垂线,垂足为E.
的平分线,交斜边AB于点D;②过点D作AC的垂线,垂足为E.
(2)在(1)作出的图形中,若![]() ,则DE= .
,则DE= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的情景对话,然后解答问题:
老师:我们新定义一种三角形,两边平方和等于第三边平方的2倍的三角形叫做奇异三角形.
小华:等边三角形一定是奇异三角形!
小明:那直角三角形是否存在奇异三角形呢?
(1)根据“奇异三角形”的定义,请你判断小华提出的命题:“等边三角形一定是奇异三角形”是真命题还是假命题?
(2)在Rt△ABC中,AB=c,AC=b,BC=a,且c>b>a,若Rt△ABC是奇异三角形,求a:b:c;
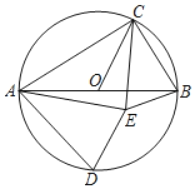
(3)如图,AB是⊙O的直径,C是⊙O上一点(不与点A、B重合),D是半圆![]() 中点,C、D在直径AB的两侧,若在⊙O内存在点E,使AE=AD,CB=CE.
中点,C、D在直径AB的两侧,若在⊙O内存在点E,使AE=AD,CB=CE.
①求证:△ACE是奇异三角形:
②当△ACE是直角三角形时,求∠AOC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】不透明的袋子中装有4个相同的小球,它们除颜色外无其它差别,把它们分别标号:1、2、3、4,
(1)随机摸出一个小球后,放回并摇匀,再随机摸出一个,用列表或画树状图的方法求出“两次取的球标号相同”的概率
(2)随机摸出两个小球,直接写出“两次取出的球标号和等于4”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:是某出租车单程收费y(元)与行驶路程x(千米)之间的函数关系图象,根据图象回答下列问题:

(1)当行使8千米时,收费应为 元;
(2)从图象上你能获得哪些信息?(请写出2条)
① ________
②____________________________
(3)求出收费y(元)与行使x(千米)(x≥3)之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班准备选一名学生参加数学史知识竞赛,现统计了两名选手本学期的五次测试 成绩:甲:83,80,90,87, 85; 乙:78,92,82,89,84.
(1)请根据上面的数据完成下表:
极差 | 平均数 | 方差 | |
甲 | 10 | ________ | ________ |
乙 | _________ | 85 | 24.8 |
(2)请你推选出一名参赛选手,并用所学的统计知识说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com