
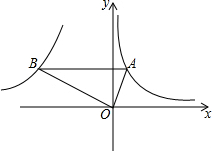
 如图,Rt△ABO中,∠AOB=90°,点A在第一象限,点B在第二象限,且AO:BO=1:2,若经过点A的反比例函数解析式为y=$\frac{1}{x}$,则经过点B(x,y)的反比例函数解析式为( )
如图,Rt△ABO中,∠AOB=90°,点A在第一象限,点B在第二象限,且AO:BO=1:2,若经过点A的反比例函数解析式为y=$\frac{1}{x}$,则经过点B(x,y)的反比例函数解析式为( )| A. | y=$\frac{2}{x}$ | B. | y=-$\frac{2}{x}$ | C. | y=-$\frac{4}{x}$ | D. | y=-$\frac{8}{x}$ |
分析 过A作AC⊥x轴于点C,过B作BD⊥x轴于点D,可证明△AOC∽△OBD,由点A在y=$\frac{1}{x}$上,可求得△AOC的面积,由相似三角形的性质可求得△BOD的面积,可求得答案.
解答 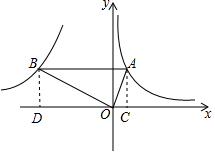 解:如图,过A作AC⊥x轴,过B作BD⊥x轴,垂足分别为C、D,
解:如图,过A作AC⊥x轴,过B作BD⊥x轴,垂足分别为C、D,
∵∠AOB=90°,
∴∠BOD+∠AOC=∠DBO+∠BOD,
∴∠DBO=∠AOC,
∴△AOC∽△OBD,
∴$\frac{{S}_{△AOC}}{{S}_{△OBD}}$=($\frac{AO}{BO}$)2=($\frac{1}{2}$)2=$\frac{1}{4}$,
设A点坐标为(xA,yA),
∵点A在函数y=$\frac{1}{x}$的图象上,
∴xAyA=1,
∴S△AOC=$\frac{1}{2}$xAyA=$\frac{1}{2}$,
∴S△OBD=4S△AOC=2,
设B点坐标为(xB,yB),
∴$\frac{1}{2}$xByB=2,
∴xByB=4,
∴过B点的反比例函数的解析式为y=-$\frac{4}{x}$,
故选C.
点评 本题主要考查待定系数法求反比例函数的解析式,相似三角形的判定和性质,根据条件求得△OBD的面积是解题的关键.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案科目:初中数学 来源: 题型:选择题
| A. | 若上升3米记作+3米,则不升不降记为0米 | |
| B. | 水位的变化是-2米,表示的意义是水位下降了-2米 | |
| C. | 温度上升-10℃是指下降10℃ | |
| D. | 盈利-10元是指亏损10元 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
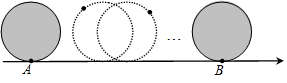 如图,半径为1个单位长度的圆从点A沿数轴向右滚动(无滑动)一周到达点B,则AB的长度为π;若点A对应的数是-1,则点B对应的数是π-1.
如图,半径为1个单位长度的圆从点A沿数轴向右滚动(无滑动)一周到达点B,则AB的长度为π;若点A对应的数是-1,则点B对应的数是π-1.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
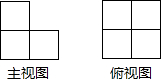 由若干个形状大小相同的小正方体组成的几何体的主视图和俯视图如图所示,则组成这个几何体的小正方体的个数至少有( )
由若干个形状大小相同的小正方体组成的几何体的主视图和俯视图如图所示,则组成这个几何体的小正方体的个数至少有( )| A. | 4个 | B. | 5个 | C. | 6个 | D. | 7个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{7}$ | B. | $\frac{3}{7}$ | C. | $\frac{4}{7}$ | D. | $\frac{5}{7}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com