
【题目】已知:如图,在长方形ABCD中,AB=4,AD=6.延长BC到点E,使CE=2,连接DE,动点P从点B出发,以每秒2个单位的速度沿BC-CD-DA向终点A运动,设点P的运动时间为![]() 秒,当
秒,当![]() 的值为_____秒时,△ABP和△DCE全等.
的值为_____秒时,△ABP和△DCE全等.
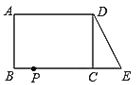
A.1B.1或3C.1或7D.3或7
科目:初中数学 来源: 题型:
【题目】已知,如图:正方形ABCD,将Rt△EFG斜边EG的中点与点A重合,直角顶点F落在正方形的AB边上,Rt△EFG的两直角边分别交AB、AD边于P、Q两点,(点P与点F重合),如图1所示:



(1)求证:EP2+GQ2=PQ2;
(2)若将Rt△EFG绕着点A逆时针旋转α(0°<α≤90°),两直角边分别交AB、AD边于P、Q两点,如图2所示:判断四条线段EP、PF、FQ、QG之间是否存在什么确定的相等关系?若存在,证明你的结论.若不存在,请说明理由;
(3)若将Rt△EFG绕着点A逆时针旋转α(90°<α<180°),两直角边所在的直线分别交BA、AD两边延长线于P、Q两点,并判断四条线段EP、PF、FQ、QG之间存在何种确定的相等关系?按题意完善图3,请直接写出你的结论(不用证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是高,E、F分别是AB、AC的中点.

(1)AB=6,AC=4,求四边形AEDF的周长;
(2)EF与AD有怎样的位置关系?证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△AEC和△DFB中,∠E=∠F,点A,B,C,D在同一直线上,有如下三个关系式:①AE∥DF,②AB=CD,③CE=BF.

(1)请用其中两个关系式作为条件,另一个作为结论,写出你认为正确的所有命题(用序号写出命题书写形式:“如果,,那么”);
(2)选择(1)中你写出的一个命题,说明它正确的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一块直角三角尺形状的木板余料,木工师傅要在此余料上锯出一块圆形的木板制作凳面,要想使锯出的凳面的面积最大.
(1)请你试着用直尺和圆规画出此圆(要求尺规作图,保留作图痕迹,不写作法).
(2)若此Rt△ABC的直角边分别为30cm和40cm,试求此圆凳面的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂甲、乙两车间接到加工一批零件的任务,从开始加工到完成这项任务共用了9天,乙车间在加工2天后停止加工,引入新设备后继续加工,直到与甲车间同时完成这项任务为止,设甲、乙车间各自加工零件总数为y(件),与甲车间加工时间x(天),y与x之间的关系如图(1)所示.由工厂统计数据可知,甲车间与乙车间加工零件总数之差z(件)与甲车间加工时间x(天)的关系如图(2)所示.

(1)甲车间每天加工零件为_____件,图中d值为_____.
(2)求出乙车间在引入新设备后加工零件的数量y与x之间的函数关系式.
(3)甲车间加工多长时间时,两车间加工零件总数为1000件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在等腰Rt△ABC中,∠BAC=90°,点E在AC上(且不与点A、C重合).在△ABC的外部作等腰Rt△CED,使∠CED=90°,连接AD,分别以AB,AD为邻边作平行四边形ABFD,连接AF.
(1)求证:△AEF是等腰直角三角形;
(2)如图2,将△CED绕点C逆时针旋转,当点E在线段BC上时,连接AE,求证:AF=![]() AE;
AE;
(3)如图3,将△CED绕点C继续逆时针旋转,当平行四边形ABFD为菱形,且△CED在△ABC的下方时,若AB=2![]() ,CE=2,求线段AE的长.
,CE=2,求线段AE的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com