练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    18．如图，在?ABCD中，过点A作AE⊥BC于点E，AF⊥DC于点F，AE=AF．
    求证：四边形ABCD是菱形．

    分析 连接AC，利用角平分线判定定理可得∠2=∠1，再利用平行线的性质可得∠DAC=∠1，利用等量代换可得∠DAC=∠2，根据等角对等边可得DA=DC，再根据邻边相等的平行四边形的菱形可得结论．

    解答 证明：连接AC，如图1．
    ∵AE⊥BC，AF⊥DC，AE=AF，
    ∴∠2=∠1，
    ∵四边形ABCD是平行四边形，
    ∴AD∥BC．
    ∴∠DAC=∠1．
    ∴∠DAC=∠2，
    ∴DA=DC，
    ∴四边形ABCD是菱形．

    点评 此题主要考查了菱形的判定，关键是掌握邻边相等的平行四边形的菱形．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    8．（1）如图，MN∥EF，GH∥EF，∠CAB=90°，∠1=70°，求：∠ABF的度数．
    （2）计算：$\sqrt{\frac{1}{9}}$+$\root{3}{\frac{26}{27}-1}$+|$\sqrt{3}$-2|-2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    9．如图，已知a∥b，直角三角板的直角顶点在直线a上，若∠1=60°，则∠2=30°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．计算：$\root{3}{-8}$+|3-$\sqrt{10}$|+$\sqrt{2+\frac{1}{4}}$-$\sqrt{0.25}$+|4-$\sqrt{10}$|．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．若2x+19的立方根是3，求3x+4的平方根．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．计算：$\sqrt{36}$×$\sqrt{\frac{1}{4}}$-$\root{3}{-8}$+$\sqrt{（-6）^{2}}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    10．八边形的内角和是（　　）
    A．900°B．1080°C．1260°D．1440°

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．如图，点D，E在AB，AC上，连接DE，DF平分∠BDE交BC于点F，∠BDF+∠DFC=180°，∠AED=∠BFD．
    （1）DE与BC平行吗？并写出理由；
    （2）写出图中与∠CED相等的角及理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

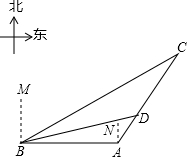    8．今年，我国海关总署严厉打击“洋垃圾”违法行动，坚决把“洋垃圾”拒于国门之外．如图，某天我国一艘海监船巡航到A港口正西方的B处时，发现在B的北偏东60°方向，相距150海里处的C点有一可疑船只正沿CA方向行驶，C点在A港口的北偏东30°方向上，海监船向A港口发出指令，执法船立即从A港口沿AC方向驶出，在D处成功拦截可疑船只，此时D点与B点的距离为75$\sqrt{2}$海里．
    （1）求B点到直线CA的距离；
    （2）执法船从A到D航行了多少海里？（结果保留根号）

    查看答案和解析>>

    同步练习册答案