
【题目】如图,AB⊥BC,DC⊥BC,E是BC上一点,使得AE⊥DE;
(1)求证:△ABE∽△ECD;
(2)若AB=4,AE=BC=5,求CD的长;
(3)当△AED∽△ECD时,请写出线段AD、AB、CD之间数量关系,并说明理由.

【答案】(1)证明见解析;(2)![]() ;(3)线段AD、AB、CD之间数量关系:AD=AB+CD;理由见解析.
;(3)线段AD、AB、CD之间数量关系:AD=AB+CD;理由见解析.
【解析】
(1)先根据同角的余角相等可得:∠DEC=∠A,利用两角相等证明三角形相似;
(2)先根据勾股定理得:BE=3,根据△ABE∽△ECD,列比例式可得结论;
(3)先根据△AED∽△ECD,证明∠EAD=∠DEC,可得∠ADE=∠EDC,证明Rt△DFE≌Rt△DCE(HL),则DF=DC,同理可得:AF=AB,相加可得结论.
(1)证明:∵AB⊥BC,DC⊥BC,
∴∠B=∠C=90°,∠BAE+∠AEB=90°,
∵AE⊥DE,
∴∠AED=90°,
∴∠AEB+∠DEC=90°,
∴∠DEC=∠BAE,
∴△ABE∽△ECD;
(2)解:Rt△ABE中,∵AB=4,AE=5,
∴BE=3,
∵BC=5,
∴EC=5﹣3=2,
由(1)得:△ABE∽△ECD,
∴![]() ,
,
∴![]() ,
,
∴CD=![]() ;
;
(3)解:线段AD、AB、CD之间数量关系:AD=AB+CD;
理由是:过E作EF⊥AD于F,
∵△AED∽△ECD,
∴∠EAD=∠DEC,
∵∠AED=∠C,
∴∠ADE=∠EDC,
∵DC⊥BC,
∴EF=EC,
∵DE=DE,
∴Rt△DFE≌Rt△DCE(HL),
∴DF=DC,
同理可得:△ABE≌△AFD,
∴AF=AB,
∴AD=AF+DF=AB+CD.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】随着“互联网+”时代的到来,传统的教学模式也在悄然发生着改变.某出国培训机构紧跟潮流,对培训课程采取了线上线下同步销售的策路,为了让客户更理性的选择,该机构推出了甲、乙两个课程体验包:甲课程体验包价值660元含3节线上课程和2节线下课;乙课程体验包价值990元含2节线上课程和5节线下课程.
(1)分别求出该机构每节课的线上价格和线下价格;
(2)该机构其中一个销售团队上个月的销售业绩为:线上课程成交900节,线下课成交1000节.为回馈客户,本月该机构针对线上、线下每节课程的价格均作出了调整:每节课线上价格比上个月的价格下调a%,线下价格比上个月的价格下调![]() a%,到本月底统计发现,该销售团队线上成交的课程数比上个月增加了
a%,到本月底统计发现,该销售团队线上成交的课程数比上个月增加了![]() a%,线下成交的课程数上升到1080节,最终团队的月销售总额线上比线下少了54000元,求a的值.
a%,线下成交的课程数上升到1080节,最终团队的月销售总额线上比线下少了54000元,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
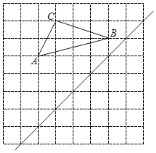
【题目】如图,在8×8的正方形网格中,每个小正方形的边长都是1,已知△ABC的三个顶点在格点上.
(1)画出△ABC关于直线l对称的△A1B1C1;
(2)在直线l上找一点P,使PA+PB的长最短;(不写作法,保留作图痕迹)
(3)△ABC 直角三角形(填“是”或“不是”),并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
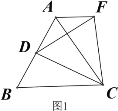
【题目】操作发现:如图1,D是等边△ABC边BA上的一动点(点D与点B不重合),连接DC,以DC为边在BC上方作等边△DCF,连接AF,易证AF=BD(不需要证明);
类比猜想:①如图2,当动点D运动至等边△ABC边BA的延长线上时,其它作法与图1相同,猜想AF与BD在图1中的结论是否仍然成立。
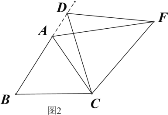
深入探究:②如图3,当动点D在等边△ABC边BA上的一动点(点D与点B不重合),连接DC,以DC为边在BC上方、下方分别作等边△DCF和等边△DCF′,连接AF,BF′你能发现AF,BF′与AB有何数量关系,并证明你发现的结论。
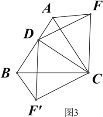
③如图4,当动点D运动至等边△ABC边BA的延长线上时,其它作法与图3相同,猜想AF,BF′与AB在上题②中的结论是否仍然成立,若不成立,请给出你的结论并证明。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在八年级(1)班学生中开展对于“我国国家公祭日”知晓情况的问卷调调查. 问卷调查的结果分为A、B、C、D四类,其中A类表示“非常了解”;B类表示“比较了解”;C类表示“基本了解”;D类表示“不太了解”;班长将本班同学的调查结果绘制成下列两幅不完整的统计图.
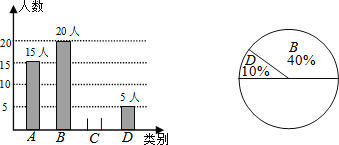
请根据上述信息解答下列问题:
(1)该班参与问卷调查的人数有 人;
(2)补全条形统计图;
(3)求C类人数占总调查人数的百分比;
(4)求扇形统计图中A类所对应扇形圆心角的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,在平面直角坐标系中,△ABC是直角三角形,∠ACB=90°,点A、C的坐标分别为A(﹣3,0),C(1,0),tan∠BAC=![]() .
.

(1)求点B的坐标;
(2)在x轴上找一点D,连接BD使得△ABD与△ABC相似(不包括全等),并求点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC中,AB=AC,∠BAC=120,
(1)利用直尺、圆规,求作AB的垂直平分线DE,交BC于点D、交AB于点E:(不要求写出作法,但要求保留作图痕迹)
(2)若BD=3,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD和矩形PEFG中,AB=8,BC=6,PE=2,PG=4.PE与AC交于点M,EF与AC交于点N,动点P从点A出发沿AB以每秒1个单位长的速度向点B匀速运动,伴随点P的运动,矩形PEFG在射线AB上滑动;动点K从点P出发沿折线PE﹣﹣EF以每秒1个单位长的速度匀速运动.点P、K同时开始运动,当点K到达点F时停止运动,点P也随之停止.设点P、K运动的时间是t秒(t>0).
(1)当t=1时,KE=_____,EN=_____;
(2)当t为何值时,△APM的面积与△MNE的面积相等?
(3)当点K到达点N时,求出t的值;
(4)当t为何值时,△PKB是直角三角形?

查看答案和解析>>
科目:初中数学 来源: 题型:
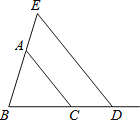
【题目】如图,已知△ABC.
(1)若AB=4,AC=5,则BC边的取值范围是 ;
(2)点D为BC延长线上一点,过点D作DE∥AC,交BA的延长线于点E,若∠E=55°,∠ACD=125°,求∠B的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com