
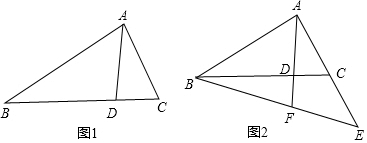
分析 (1)由CA2=CD•CB知CA:CD=CB:CA,根据∠C=∠C证△CAB∽△CDA即可得;
(2)过点B作BG∥AE,交AF的延长线于点G,由△ACD∽△BCA知∠CAD=∠CBA,结合BG∥AE,即∠G=∠CAD,得∠G=∠CBA,证△ABD∽△AGB得$\frac{AB}{GB}=\frac{AD}{BD}$,由BG∥AE知$\frac{EF}{BF}$=$\frac{AE}{GB}$=$\frac{AB}{GB}$,从而得证$\frac{EF}{BF}$=$\frac{AD}{BD}$.
解答 证明:(1)∵CA2=CD•CB,
∴CA:CD=CB:CA
∵∠C=∠C,
∴△CAB∽△CDA,
∴$\frac{AD}{AB}$=$\frac{AC}{BC}$;
(2)如图,过点B作BG∥AE,交AF的延长线于点G,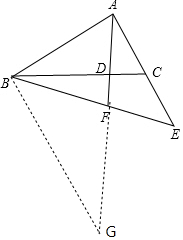
∵△ACD∽△BCA,
∴∠CAD=∠CBA,
∵BG∥AE,
∴∠G=∠CAD,
∴∠G=∠CBA,
又∠BAD=∠GAB,
∴△ABD∽△AGB,
∴$\frac{AD}{AB}$=$\frac{BD}{GB}$,即$\frac{AB}{GB}=\frac{AD}{BD}$,
∵BG∥AE,
∴$\frac{EF}{BF}$=$\frac{AE}{GB}$,
又∵AE=AB,
∴$\frac{EF}{BF}$=$\frac{AB}{GB}$,
∴$\frac{EF}{BF}$=$\frac{AD}{BD}$.
点评 本题主要考查相似三角形的判定与性质,通过构建△ABD∽△AGB将$\frac{EF}{BF}$与$\frac{AD}{BD}$通过$\frac{AE}{BG}$联系到一起是解题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 吉安市机关公车改革于今年4月1日正式开始实施,小明坐着爸爸新买的小车,在闹市区街道边发现一块标志牌(如图所示),小明知道这表示车速不超过这个字,请你用式子表示在该车道上车辆行驶速度v(km/h)的数值范围:v≤10.
吉安市机关公车改革于今年4月1日正式开始实施,小明坐着爸爸新买的小车,在闹市区街道边发现一块标志牌(如图所示),小明知道这表示车速不超过这个字,请你用式子表示在该车道上车辆行驶速度v(km/h)的数值范围:v≤10.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com