【题目】从南京站开往上海站的一辆和谐号动车，中途只停靠苏州站，甲、乙、丙3名互不相识的旅客同时从南京站上车．
（1）求甲、乙、丙三名旅客在同一个站下车的概率；
（2）求甲、乙、丙三名旅客中至少有一人在苏州站下车的概率．
【答案】
（1）解：画树状图得：
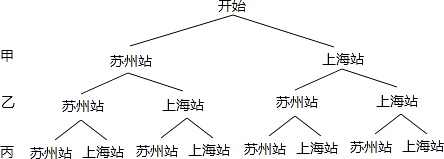
∵共有8种等可能的结果，甲、乙、丙三名旅客在同一个站下车的有2种情况，
∴甲、乙、丙三名旅客在同一个站下车的概率为： 
= 
（2）解：∵甲、乙、丙三名旅客中至少有一人在苏州站下车的有7种情况；
∴甲、乙、丙三名旅客中至少有一人在苏州站下车的概率为： 
【解析】（1）首先根据题意画出树状图，然后由树状图求得所有等可能的结果与甲、乙、丙三名旅客在同一个站下车的情况，再利用概率公式即可求得答案；（2）由（1）可求得甲、乙、丙三名旅客中至少有一人在苏州站下车的有7种情况；，然后利用概率公式求解即可求得答案．
【考点精析】解答此题的关键在于理解列表法与树状图法的相关知识，掌握当一次试验要设计三个或更多的因素时，用列表法就不方便了，为了不重不漏地列出所有可能的结果，通常采用树状图法求概率．
科目：初中数学 来源： 题型：
【题目】如图，已知一次函数的图象y=kx+b与反比例函数y=﹣ 
的图象交于A，B两点，且点A的横坐标和点B的纵坐标都是﹣2，求： 
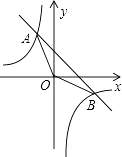
（1）一次函数的解析式；
（2）△AOB的面积；
（3）直接写出一次函数的函数值大于反比例函数的函数值时x的取值范围．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】我校“文化氧吧”有A、B、C、D四本书是小明想拜读的，但他现阶段只打算选读两本．
（1）若小明已选A书，再从其余三本书中随机选一款，恰好选中C的概率是；
（2）小明随机选取两本书，请用树状图或列表法求出他恰好选中A、C两本的概率．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在数轴上点A、B、C表示的数分别为﹣2、1、6，点A与点B之间的距离表示为AB，点B与点C之间的距离表示为BC，点A与点C之间的距离表示为AC
（1）请直接写出AB、BC、AC的长度；
（2）若点D从A点出发，以每秒1个单位长度的速度向左运动，点E从B点出发以每秒2个单位长度的速度向右运动，点F从C点出发以每秒5个单位长度的速度向右运动．设点D、E、F同时出发，运动时间为t秒，试探索：EF﹣DE的值是否随着时间t的变化而变化？请说明理由．
（3）若点M以每秒4个单位的速度从A点出发，点N以每秒3个单位的速度运动从C点出发，设点M、N同时出发，运动时间为t秒，试探究：经过多少秒后，点M、N两点间的距离为14个单位．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图(甲)，在正方形
中，
是
上一点，
是
延长线上一点，且
．
(1)求证:
；
(2)在如图(甲)中，若
在上，且
，则
成立吗？
证明你的结论．(3)运用(1)(2)解答中积累的经验和知识，完成下题:
如图(乙)四边形中，∥
(＞)，
，
,点是上一点，且
，
，求
的长．
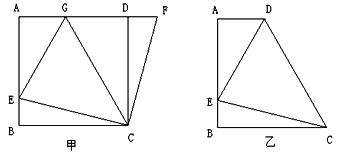
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系中．过一点分別作坐标轴的垂线，若与坐标轴围成矩形的周长的数值与面积的数值相等，则这个点叫做和谐点．例如．图中过点P分別作x轴，y轴的垂线．与坐标轴围成矩形OAPB的周长的数值与面积的数值相等，则点P是和谐点．
（1）判断点M（1，2），N（4，4）是否为和谐点，并说明理由；
（2）若和谐点P（a，3）在直线y=﹣x+b（b为常数）上，求a，b的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
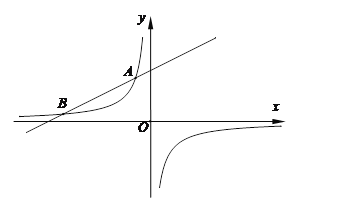
【题目】如图，反比例函数
与一次函数
的图象交于点A（－2，6）、点B（
，1）.
（1）求反比例函数与一次函数的表达式；
（2）点E为y轴上一个动点，若S△AEB=5，求点E的坐标．
（3）将一次函数的图象沿
轴向下平移n个单位，使平移后的图象与反比例函数的图象有且只有一个交点，求n的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
