练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    4．已知|x-y|=y-x，|x|=3，y=2，则（x+y）3=-125．

    分析 先求出x、y的值，再代入代数式进行计算即可．

    解答 解：∵|x-y|=y-x，
    ∴x-y＜0，即x＜y．
    ∵|x|=3，y=2，
    ∴x=±3．
    ∵x＜y，
    ∴x=-3，y=2，
    ∴（x+y）3=（-3-2）3=-125．
    故答案为：-125．

    点评 本题考查的是有理数的乘方，熟知乘方的法则是解答此题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    6．下列说法正确的是（　　）
    A．两直线平行，同旁内角可能相等
    B．同底数幂相乘，底数相乘，指数相加
    C．一个图形和它经过平移所得的图形中，两组对应点的连线一定平行
    D．任何数的0次幂等于1

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

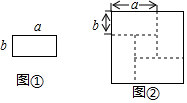    7．小翠利用如图①所示的长为a、宽为b的长方形卡片4张，拼成了如图②所示的图形，则根据图②的面积关系能验证的恒等式为（　　）
    A．（a-b）2+4ab=（a+b）2B．（a-b）（a+b）=a2-b2C．（a+b）2=a2+2ab+b2D．（a-b）2=a2-2ab+b2

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．计算：（$\sqrt{3}$-6）0-（-$\frac{1}{5}$）-1-3tan30°+|-$\sqrt{3}$|

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．如图，在平面直角坐标系中，A、C两点在坐标轴上，Rt△ACO绕点原点O顺时针旋转90°后得到△DBO，OC=3，抛物线y=-x2+bx+c经过点A、B、C．
    （1）求抛物线的解析式；
    （2）在抛物线对称轴上，是否存在这样的点P，使PA+PD得最小值？若存在，请求出点P点的坐标；若不存在，请说明理由．
    （3）在抛物线上有一点Q，使得△QBD是以BD为直角边的直角三角形，请直接写出Q点的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    9．周长为10cm的长方形的一边长为xcm，其面积y（cm2）与x（cm）之间的关系式为y=$\frac{（10-x）x}{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

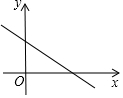    16．如果一次函数的图象如图所示，则它的表达式可能是（　　）
    A．y=$\frac{2}{3}$xB．y=-$\frac{2}{3}$xC．$\frac{2}{3}$x+1=yD．1-$\frac{2}{3}$x=y

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．阅读下列材料，并解决相应问题：
    $\frac{2}{\sqrt{5}-\sqrt{3}}$=$\frac{2（\sqrt{5}+\sqrt{3}）}{（\sqrt{5}-\sqrt{3}）（\sqrt{5}+\sqrt{3}）}$=$\frac{2（\sqrt{5}+\sqrt{3}）}{2}$=$\sqrt{5}$$+\sqrt{3}$
    应用：用上述类似的方法化简下列各式：
    （1）$\frac{1}{\sqrt{7}+\sqrt{6}}$
    （2）若a是$\sqrt{2}$的小数部分，求$\frac{3}{a}$的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

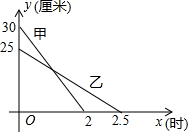    14．在一次蜡烛燃烧实验中，甲、乙两根蜡烛燃烧时所剩余部分的高度y（cm）与燃烧时间x（h）的关系如图所示，请根据图象提供的信息解答下列问题：
    （1）甲、乙两根蜡烛燃烧前的高度分别是30cm、25cm，从点燃到烧尽所用小时分别是2h、2.5h
    （2）分别求出甲、乙两根蜡烛燃烧时，y与x之间的函数解析式；
    （3）当x为何值时，甲、乙两根蜡烛在燃烧过程中的高度相等？

    查看答案和解析>>

    同步练习册答案