
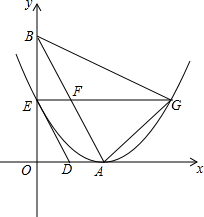
 ��ͼ��ֱ��y=-$\sqrt{3}$x+2$\sqrt{3}$��x�ᡢx��ֱ��ڵ�A��B��������D��E�ֱ��A��Bͬʱ�������O�˶����˶���O��ֹͣ�����˶��ٶȷֱ���1����λ����/���$\sqrt{3}$����λ����/�룬���˶�ʱ��Ϊt�룬�Ե�AΪ����������߾�����E������E��x���ƽ���ߣ��������ߵ���һ������ΪG�㣬��AB�ཻ�ڵ�F��
��ͼ��ֱ��y=-$\sqrt{3}$x+2$\sqrt{3}$��x�ᡢx��ֱ��ڵ�A��B��������D��E�ֱ��A��Bͬʱ�������O�˶����˶���O��ֹͣ�����˶��ٶȷֱ���1����λ����/���$\sqrt{3}$����λ����/�룬���˶�ʱ��Ϊt�룬�Ե�AΪ����������߾�����E������E��x���ƽ���ߣ��������ߵ���һ������ΪG�㣬��AB�ཻ�ڵ�F������ ��1����ֱ��y=-$\sqrt{3}$x+2$\sqrt{3}$�У��ֱ���y=0��x=0���������A��B�������ꣻ
��2����OA��OB�ij�����á�ABO=30�㣬��t�ɱ�ʾ��BE��EF����BF�ij����ɹ��ɶ��������AB�ij����Ӷ�����t��ʾ��AF�ij���
��3���������ε����ʿ����t��ֵ��������AF=AG�ij����ɵõ�$\frac{AF}{AG}=\frac{AG}{AB}$�����ж���AFG���AGB���ƣ�
��4���ȵó���DAF=60�㣬�ٷ���������á�DAF������ֵ����������⼴�ɵó����ۣ�
��� �⣺��1����ֱ��y=-$\sqrt{3}$x+2$\sqrt{3}$�У�
��y=0���ɵ�0=-$\sqrt{3}$x+2$\sqrt{3}$�����x=2��
��x=0���ɵ�y=2$\sqrt{3}$��
��A��2��0����B��0��2$\sqrt{3}$����
��2���ɣ�1����֪OA=2��OB=2$\sqrt{3}$��
��tan��ABO=$\frac{OA}{OB}$=$\frac{\sqrt{3}}{3}$��
���ABO=30�㣬
���˶�ʱ��Ϊt�룬
��BE=$\sqrt{3}$t��
��EF��x�ᣬ
����Rt��BEF�У�EF=BE•tan��ABO=$\frac{\sqrt{3}}{3}$BE=t��BF=2EF=2t��
��Rt��ABO��OA=2��OB=2$\sqrt{3}$��
��AB=4��
��AF=4-2t��
��3�����ƣ��������£�
���ı���ADEFΪ����ʱ������EF=AF��
��t=4-2t�����t=$\frac{4}{3}$��
��AF=4-2t=4-$\frac{8}{3}$=$\frac{4}{3}$��OE=OB-BE=2$\sqrt{3}$-$\sqrt{3}$��$\frac{4}{3}$=$\frac{2\sqrt{3}}{3}$��
��ͼ����G��GH��x�ᣬ��x���ڵ�H��
���ı���OEGHΪ���Σ�
��GH=OE=$\frac{2\sqrt{3}}{3}$��
��EG��x�ᣬ�����ߵĶ���ΪA��
��OA=AH=2��
��Rt��AGH�У��ɹ��ɶ����ɵ�AG2=GH2+AH2=$��\frac{2\sqrt{3}}{3}��^{2}+{2}^{2}$=$\frac{16}{3}$��
��AF•AB=$\frac{4}{3}$��4=$\frac{16}{3}$��
��AF•AB=AG2��
��$\frac{AF}{AG}=\frac{AG}{AB}$���ҡ�FAG=��GAB��
���AFG�ס�AGB��
��4�����ڣ�
���ɣ���A��2��0����
���������ߵĽ���ʽΪy=a��x-2��2��
���˶�֪��BE=$\sqrt{3}$t��AD=t��OE=2$\sqrt{3}$-$\sqrt{3}$t��
��F��t��2$\sqrt{3}$-$\sqrt{3}$t����D��2-t��0����E��0��$\sqrt{3}$t��
��A��2��0����
��DF=$\sqrt{��2-t-t��^{2}+��2\sqrt{3}-\sqrt{3}t��^{2}}$=$\sqrt{7{t}^{2}-20t+16}$��AF=$\sqrt{��t-2��^{2}+��2\sqrt{3}-\sqrt{3}t��^{2}}$=$\sqrt{4{t}^{2}-16t+16}$
��Rt��AOB��tan��OAB=$\frac{OB}{OA}$=$\sqrt{3}$��
���DAF=60�㣬
�ߡ�ADFΪֱ�������Σ�
��ٵ���ADF=90��ʱ��
��Rt��ADF��tan��DAF=$\frac{DF}{AD}$=$\frac{OE}{AD}$=$\frac{2\sqrt{3}-\sqrt{3}t}{t}$=$\sqrt{3}$��
��t=1��
��E��0��$\sqrt{3}$����
���˵�E��������������ߵĽ���ʽΪy=a��x-2��2��
�ã�$\sqrt{3}$=4a��
��a=$\frac{\sqrt{3}}{4}$��
�������ߵĽ���ʽΪy=$\frac{\sqrt{3}}{4}$��x-2��2��
�ڵ���AFD=90��ʱ��
��Rt��ADF��tan��DAF=$\frac{DF}{AF}$=$\frac{\sqrt{7{t}^{2}-20t+16}}{\sqrt{4{t}^{2}-16t+16}}$=$\sqrt{3}$��
��t=$\frac{8}{5}$��t=4���ᣩ��
��E��0��$\frac{8\sqrt{3}}{5}$����
���˵�E��������������ߵĽ���ʽΪy=a��x-2��2��
�ã�$\frac{8}{5}$$\sqrt{3}$=4a��
��a=$\frac{2\sqrt{3}}{5}$��
�������ߵĽ���ʽΪy=$\frac{2\sqrt{3}}{5}$��x-2��2��
�������������������߽���ʽΪy=$\frac{\sqrt{3}}{4}$��x-2��2����y=$\frac{2\sqrt{3}}{5}$��x-2��2��
���� ����Ϊ���κ������ۺ�Ӧ�ã��漰֪ʶ���д���ϵ���������Ǻ����Ķ��塢���������ε��ж������ʡ����ɶ��������κ����ĶԳ��Եȣ��ڣ�2������á�ABO=30���ǽ���Ĺؼ����ڣ�3�������t��ֵ����ʾ��AG�ij����ǽ���Ĺؼ������⿼��֪ʶ��϶࣬�ۺ��Խ�ǿ���ѶȽϴ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -9 | B�� | $-\frac{1}{9}$ | C�� | C��$\frac{1}{9}$ | D�� | 9 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���߶�AC��BD���ڵ�M����B��D����ֱ���AC�Ĵ��߶�BF��DE��AB=CD
��ͼ���߶�AC��BD���ڵ�M����B��D����ֱ���AC�Ĵ��߶�BF��DE��AB=CD�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��GΪBC���е㣬��DG��BC��DE��AB��E��DF��AC��F��BE=CF��
��ͼ��GΪBC���е㣬��DG��BC��DE��AB��E��DF��AC��F��BE=CF���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
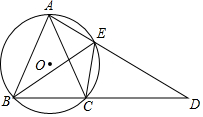 ��ͼ����ABC�ڽ��ڡ�O����AB=AC���ӳ�BC����D��ʹCD=AC������AD����O���ڵ�E������BE��CE��
��ͼ����ABC�ڽ��ڡ�O����AB=AC���ӳ�BC����D��ʹCD=AC������AD����O���ڵ�E������BE��CE���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com