
分析 (1)计算张师傅行驶的路程的代数和即可,
(2)计算出每段路程的绝对值的和后乘以a,即为这天上午汽车共耗油数;
(3)表示出每段的收入后计算它们的和即为上午的收入.
解答 解:(1)(+8)+(-6)+(+3)+(-7)+(+2)
=8-6+3-7+2
=0千米.
答:将最后一名乘客送到目的地,张师傅正好回到出车地点.
(2)(8+6+3+7+2)×a=26a升.
答:这天午共耗油26a升.
(3)[10+(8-3)×2]+[10+(6-3)×2]+10+[10+(7-3)×2]+10=74元.
答:张师傅这天上午的收入一共是74元.
点评 此题考查了正数和负数,本题利用了有理数中的加法和乘法运算,注意要针对不同情况用不同的计算方法.


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
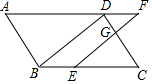 如图,在平行四边形ABCD中,点E在边BC上,过点E作BD的平行线交DC于点G、交AD的延长线于点F.
如图,在平行四边形ABCD中,点E在边BC上,过点E作BD的平行线交DC于点G、交AD的延长线于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图在数轴上A点表示数a,B点表示数b,a、b满足|a+2|+|b-4|=0.
如图在数轴上A点表示数a,B点表示数b,a、b满足|a+2|+|b-4|=0.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com