
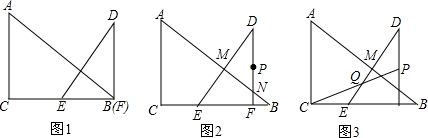
分析 (1)作出此时的图形,由平移性质可知BF就是运动的路程,用t表示出BF,再利用相似三角形的线段比例关系列出方程,解之即可;
(2)求重叠部分面积的关键是要弄清楚重叠部分的几何形状,观察△DEF的整个运动过程可以发现:0<t≤6重叠部分是一个四边形,6<t≤$\frac{32}{3}$重叠部分是一个五边形,$\frac{32}{3}$<t≤12重叠部分是一个直角梯形,对三种情况分别用割补法求之即可;
(3)①△PMN要为等腰三角形,分PN=PM,NP=NM,MP=MN三种情况分别计算即可.
②要求Q点所经过的路径的长度,也就是求运动过程中Q点的轨迹的长度.既然要求轨迹,那么首先要弄清楚轨迹的形状.此问的难点在于P点同时具有水平方向与竖直方向上的速度,这使得问题有点“偏物理”,给分析也带来一定难度.对于这个问题,有以下两种处理思路:
第一种,利用极端原理简化处理,由于运动都是匀速直线动,所以我们可以断定Q点的路径是直线型的,这样以来,我们就可简化处理,也就是不必关心中间过程,找到初始时刻Q点的位置(就是BC的中点),再找到终点时刻(即P点到达D点时)Q点的位置,连接起始点与终点线段就是Q点的路径长度,.
第二种,对于上一种,虽然可以算出正确答案,但总感觉逻辑上有所欠缺,因为我们事先断定轨迹是直的而不是曲的.本质上讲这是一个轨轨问题,需要借助解析手段才能严格说明为什么Q点的轨迹是直的而不是弯的.为此,我们以C点为坐标原点,CA为y轴,CB为x轴建立坐标系,将P点的坐标用t表示,Q点的坐标也可以用t表示,这样我们清晰地说明Q点始终在一直线上,这条直线的解析式也是可以求出来的,整个运动过程的时间也就是P点走完FD所用的时间,即4秒,这样Q点轨迹长度就迎刃而解了.
解答 解:(1)如图D1,当D点落在AB上时,
tan∠ABC=$\frac{DF}{BF}=\frac{AC}{BC}$,
即$\frac{8}{t}=\frac{9}{12}$,解得$t=\frac{32}{3}$(秒).
(2)当0<t≤6时,如图D2-1,此时重叠部分为四边形GHEF,且S=S△BEG-S△BFH,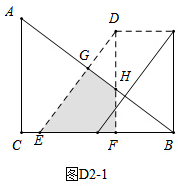
∵AC=9,BC=12,
∴AB=15,
∴sin∠ABC=$\frac{9}{15}=\frac{3}{5}$,
∵EG=$\frac{3}{5}$BE=$\frac{3}{5}$(6+t),
BG=$\frac{4}{5}$BE=$\frac{4}{5}$(6+t),
∴S△BEG=$\frac{1}{2}$BG×EG=$\frac{6}{25}$(6+t)2,
∵FH=$\frac{3}{4}$BF=$\frac{3}{4}$t,
∴S△BFH=$\frac{1}{2}$BF×FH=$\frac{3}{8}$t2,
∴S=S△BEG-S△BFH=$\frac{6}{25}$(6+t)2-$\frac{3}{8}$t2=-$\frac{27}{200}$t2+$\frac{72}{25}$t+$\frac{216}{25}$;
当6<t≤$\frac{32}{3}$时,如图D2-2,此时重叠部分为五边形JKFCL,且S=S梯KFCA-S△AJL,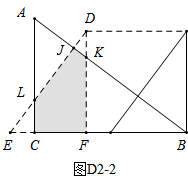
∵BF=t,
KF=$\frac{3}{4}$t,
CF=12-t,
CE=t-6,
CL=$\frac{4}{3}$CE=$\frac{4}{3}$(t-6),
AL=AC-CL=9-$\frac{4}{3}$(t-6)=-$\frac{4}{3}$t+17,
AJ=$\frac{3}{5}$AL=-$\frac{4}{5}$t+$\frac{51}{5}$,
LJ=$\frac{4}{5}$AL=-$\frac{16}{15}$t+$\frac{68}{5}$,
∴S梯KFCA=$\frac{1}{2}$(KF+AC)×CF=$\frac{1}{2}$($\frac{3}{4}$t+9)×(12-t)=-$\frac{3}{8}$t2+54,
S△AJL=$\frac{1}{2}$AJ×LJ=$\frac{1}{2}$(-$\frac{4}{5}$t+$\frac{51}{5}$)(-$\frac{16}{15}$t+$\frac{68}{5}$)=$\frac{32}{75}$t2-$\frac{816}{75}$t+$\frac{1734}{25}$,
∴S=S梯KFCA-S△AJL=-$\frac{3}{8}$t2+54-($\frac{32}{75}$t2-$\frac{816}{75}$t+$\frac{1734}{25}$)=-$\frac{481}{600}$t2+$\frac{816}{75}$t-$\frac{384}{25}$,
当$\frac{32}{3}$<t≤12时,如图D2-3,此时重叠部分为直角梯形DFCO,
∵CE=t-6,
CO=$\frac{4}{3}$CE=$\frac{4}{3}$(t-6),
CF=12-t,
∴S=S△DEF-S△CEO=$\frac{1}{2}$×8×6-$\frac{1}{2}$×(t-6)×$\frac{4}{3}$(t-6)=-$\frac{2}{3}$t2+8t,
综合所述,S=$\left\{\begin{array}{l}{-\frac{27}{200}{t}^{2}+\frac{72}{25}t+\frac{216}{25}(0<t≤6)}\\{-\frac{481}{600}{t}^{2}+\frac{816}{75}t-\frac{384}{25}(6<t≤\frac{32}{3})}\\{-\frac{2}{3}{t}^{2}+8t(\frac{32}{3}<t≤12)}\end{array}\right.$
(3)①Ⅰ、若PM=PN,如图D3-1-1,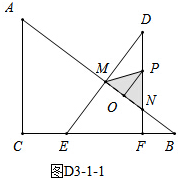
∵BF=t,
NF=$\frac{3}{4}$t,
BN=$\frac{5}{4}$t,
BE=6+t,
BM=$\frac{4}{5}$(6+t),
∴MN=BM-BN=$\frac{4}{5}$(6+t)-$\frac{5}{4}$t=-$\frac{9}{20}$t+$\frac{24}{5}$,
作PT⊥MN于T,MT=NT=$\frac{1}{2}$MN=-$\frac{9}{40}$t+$\frac{12}{5}$,
∵PF=2t,PN=PF-NF=2t-$\frac{3}{4}$t=$\frac{5}{4}$t,
∴$\frac{NT}{PN}=\frac{NF}{BN}=\frac{3}{5}$,
即NT=$\frac{3}{5}$PN,
-$\frac{9}{40}$t+$\frac{12}{5}$=$\frac{3}{4}$t,解得t=$\frac{32}{13}$
Ⅱ、若NP=NM,如图D3-1-2,
∵BF=t,
NF=$\frac{3}{4}$t,
BN=$\frac{5}{4}$t,
BE=6+t,
BM=$\frac{4}{5}$(6+t),
∴MN=BM-BN=$\frac{4}{5}$(6+t)-$\frac{5}{4}$t=-$\frac{9}{20}$t+$\frac{24}{5}$,
∵PF=2t,PN=PF-NF=2t-$\frac{3}{4}$t=$\frac{5}{4}$t,
∴$\frac{5}{4}$t=-$\frac{9}{20}$t+$\frac{24}{5}$,解得t=$\frac{48}{17}$
Ⅲ、若MP=MN,如图D3-1-3,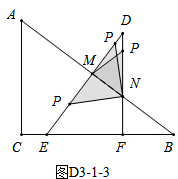
当P在DN上时:
∵MN=-$\frac{9}{20}$t+$\frac{24}{5}$,
DN=$\frac{5}{3}$MN,
PD=8-2t,
PN=2×$\frac{3}{5}$MN=$\frac{6}{5}$MN,
DN=PN+PD,
$\frac{5}{3}$MN=8-2t+$\frac{6}{5}$MN,
$\frac{7}{15}$MN=8-2t,
$\frac{7}{15}$(-$\frac{9}{20}$t+$\frac{24}{5}$)=8-2t,解得:t=$\frac{576}{179}$;
当P点在MD上时:
∵MN=-$\frac{9}{20}$t+$\frac{24}{5}$,
MD=$\frac{4}{3}$MN,
PD=2t-8,
MP=MD-PD=$\frac{4}{3}$MN-2t+8,
MN=$\frac{4}{3}$MN-2t+8,
$\frac{1}{3}$(-$\frac{9}{20}$t+$\frac{24}{5}$)-2t+8=0,解得t=$\frac{192}{43}$;
当P点在ME上时:
∵MN=-$\frac{9}{20}$t+$\frac{24}{5}$,
MD=$\frac{4}{3}$MN,
PD=2t-8,
MP=2t-MD-8=2t-$\frac{4}{3}$MN-8,
∴MN=2t-$\frac{4}{3}$MN-8,
$\frac{7}{3}$(-$\frac{9}{20}$t+$\frac{24}{5}$)=2t-8,解得t=$\frac{384}{61}$.
综上所述,当t的值为$\frac{32}{13}$、$\frac{48}{17}$、$\frac{576}{179}$、$\frac{192}{43}$、$\frac{384}{61}$时,△PMN是等腰三角形.
②方法一:(极端原理)
在起始时刻,P点、F点都与B点重合,如图D3-2-1,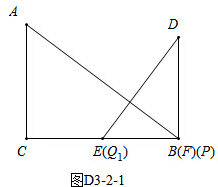
此时,CP的中点就是BC的中点Q1,
当P点从F点运动到D点时,如图D3-2-2,
∵t=$\frac{DF}{2}$=4(秒),
BF=4,CF=12-4=8=DF,
∴△CPF是等腰直角三角形,
∴∠PCF=45°,
过Q2作Q2S⊥BC于S,
∵Q2是中点,
∴Q2S=$\frac{1}{2}$DF=4,
CS=Q2S=4,
Q1S=CQ1-CS=6-4=2,
∴Q1Q2=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$,
方法二:(解析法)
如图D3-2-3,以C点为坐标原点,CA为y轴,CB为x轴建立坐标系,
则P点的坐标为(12-t,2t),Q点的坐标为($\frac{12-t}{2}$,t),
令$\left\{\begin{array}{l}{x=\frac{12-t}{2}}\\{y=t}\end{array}\right.$,消去t可得,y=-2x+12,
即Q点始终在直线l:y=-2x+12上运动,说明Q点的轨迹是一条直线段.
令t=0,得到Q点的初始位置的坐标为Q1(6,0),
令t=4,得到Q点的终点位置的坐标为Q2(4,4),
作过Q2作Q2S⊥BC于R,则Q2R=4,Q1R=2,
∴Q1Q2=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$.
综上所述,线段CP的中点Q所经过的路径长度为2$\sqrt{5}$.
点评 本题以动态几何为背景,综合考查了相似三角形、三角函数、面积计算、等腰三角形的性质、分类讨论、勾股定理等多个知识点和技能,计算过程宏大复杂,难度很大,对同学们的数学素质要求极高.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源: 题型:解答题
 一次函数的图象经过点A(2,0)、B(0,-2$\sqrt{3}$),P为直线AB上的动点,
一次函数的图象经过点A(2,0)、B(0,-2$\sqrt{3}$),P为直线AB上的动点,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
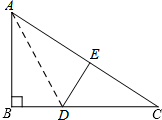 如图,在Rt△ABC中,∠ABC=90°,AC=10,BC=8,AD是∠BAC的平分线,点E是斜边AC上的一点,且AE=AB,沿△DEC的一个内角平分线折叠,使点C落在DE所在直线上,则折痕的长度为$\frac{12\sqrt{2}}{7}$和$\frac{3\sqrt{5}}{2}$.
如图,在Rt△ABC中,∠ABC=90°,AC=10,BC=8,AD是∠BAC的平分线,点E是斜边AC上的一点,且AE=AB,沿△DEC的一个内角平分线折叠,使点C落在DE所在直线上,则折痕的长度为$\frac{12\sqrt{2}}{7}$和$\frac{3\sqrt{5}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
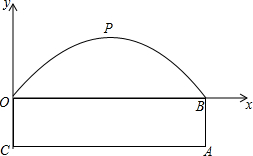 如图所示,某隧道横截面的轮廓线由抛物线对称的一部分和矩形的一部分组成,最大高度为6米,底部宽度为12米,OC=3米,现如图建立平面直角坐标系.
如图所示,某隧道横截面的轮廓线由抛物线对称的一部分和矩形的一部分组成,最大高度为6米,底部宽度为12米,OC=3米,现如图建立平面直角坐标系.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com