
【题目】如图,已知抛物线经过A(﹣2,0),B(﹣3,3)及原点O,顶点为C.

(1)求抛物线的函数解析式.
(2)设点D在抛物线上,点E在抛物线的对称轴上,若四边形AODE是平行四边形,求点D的坐标.
(3)联接BC交x轴于点F.y轴上是否存在点P,使得△POC与△BOF相似?若存在,求出点P的坐标;若不存在,请说明理由.
【答案】(1) y=x2+2x;(2) (1,3);(3) (0,﹣ ![]() )或(0,﹣4).
)或(0,﹣4).
【解析】试题分析:(1)将点A、点B和原点代入解析式进行求解;(2)根据平行四边形的性质得出点D的坐标;(3)首先求出OB、OF、OC的长度,然后根据三角形相似的条件求出点P的坐标,分两种情况进行讨论.
试题解析:(1)设抛物线的解析式为y=ax2+bx+c(a≠0),
将点A(﹣2,0),B(﹣3,3),O(0,0),代入可得: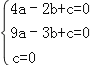 ,解得:
,解得:![]() ,
,
所以函数解析式为:y=x2+2x;
(2)∵AO为平行四边形的一边, ∴DE∥AO,DE=AO, ∵A(﹣2,0),
∴DE=AO=2, ∵四边形AODE是平行四边形, ∴D在对称轴直线x=﹣1右侧,
∴D横坐标为:﹣1+2=1,代入抛物线解析式得y=3, ∴D的坐标为(1,3);
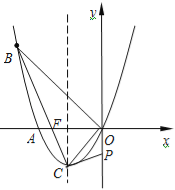
(3)在y轴上存在点P,使得△POC与△BOF相似,理由如下:
由y=x2+2x,顶点C的坐标为(﹣1,1) ∵tan∠BOF=![]() ,
,
∴∠BOF=45°, 当点P在y轴的负半轴时,tan∠COP=![]() ,
,
∴∠COP=45°,∴∠BOF=∠COP, 设BC的解析式为y=kx+b(k≠0),
∵图象经过B(﹣3,3),C(﹣1,1)
∴![]() , 解得∴
, 解得∴![]() ,
,
∴y=﹣2x﹣3; 令y=0,则x=﹣1.5.
∴F(﹣1.5,0),
∴OB=3![]() ,OF=1.5,OC=
,OF=1.5,OC=![]() ,
,
①当△POC∽△FOB时, 则![]() ,
,
即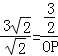 , ∴OP=
, ∴OP=![]() , ∴P(0,﹣
, ∴P(0,﹣![]() )
)
②当△POC∽△BOF时, ∴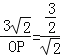 ,
,
∴OP=4, ∴P(0,﹣4),
∴当△POC与△BOF相似时,点P的坐标为(0,﹣![]() )或(0,﹣4).
)或(0,﹣4).


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】△ABC中,∠C=60°,点D,E分别是边AC,BC上的点,点P是直线AB上一动点,连接PD,PE,设∠DPE=α.
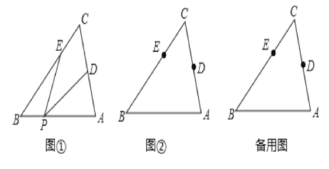
(1)如图①所示,如果点P在线段BA上,且α=30°,那么∠PEB+∠PDA=___;
(2)如图②所示,如果点P在线段BA上运动,
①依据题意补全图形;
②写出∠PEB+∠PDA的大小(用含α的式子表示);并说明理由。
(3)如果点P在线段BA的延长线上运动,直接写出∠PEB与∠PDA之间的数量关系(用含α的式子表示).那么∠PEB与∠PDA之间的数量关系是___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)操作发现:
如图,在矩形ABCD中,E是BC的中点,将△ABE沿AE折叠后得到△AFE,点F在矩形ABCD内部,延长AF交CD于点G.猜想线段GF与GC有何数量关系?并证明你的结论.

(2)类比探究:
如图,将(1)中的矩形ABCD改为平行四边形,其它条件不变,(1)中的结论是否仍然成立?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
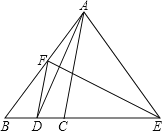
【题目】如图,在△ABC中,AD是∠BAC的平分线,AD的垂线平分线交AB于点F,交BC的延长线于点E,连接AE,DF.
求证:(1)∠EAD=∠EDA;(2)DF//AC;(3)∠EAC=∠B.
查看答案和解析>>
科目:初中数学 来源: 题型:
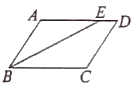
【题目】如图已知BE平分∠ABC,E点在线段AD上,∠ABE=∠AEB,AD与BC平行吗?为什么?
解:因为BE平分∠ABC(已知)
所以∠ABE=∠EBC ( )
因为∠ABE=∠AEB( )
所以∠ =∠ ( )
所以AD∥BC ( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的边BC在x轴上,顶点A在y轴的正半轴上,OA=2,OB=1,OC=4.
(1)求过A、B、C三点的抛物线的解析式;
(2)设点M是x轴上的动点,试问:在平面直角坐标系中,是否存在点N,使得以点A,B,M,N为顶点的四边形是菱形?若存在,直接写出点N的坐标;若不存在,说明理由;
(3)若抛物线对称轴交x轴于点P,在平面直角坐标系中,是否存在点Q,使△PAQ是以PA为腰的等腰直角三角形?若存在,写出所有符合条件的点Q的坐标,选择一种情况加以说明;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学举行“汉字听写”比赛,每位学生听写汉字![]() 个,比赛结束后,随机抽查部分学生的听写结果,以下是根据抽查结果绘制的统计图的一部分,根据信息解决下列问题:
个,比赛结束后,随机抽查部分学生的听写结果,以下是根据抽查结果绘制的统计图的一部分,根据信息解决下列问题:
组别 | 正确字数 | 人数 |
A |
|
|
B |
|
|
C |
|
|
D |
|
|
E |
|
|


(1)在统计表中,![]() ,
,![]() ;
;
(2)补全条形统计图;
(3)在扇形统计图中“D组”所对应的圆心角的度数为 ;
(4)若该校共有![]() 名学生,如果听写正确的字数少于
名学生,如果听写正确的字数少于![]() 个定为不合格,请你估计这所中学这次比赛听写不合格的学生人数.
个定为不合格,请你估计这所中学这次比赛听写不合格的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知矩形ABCD中,E是AD边上的一个动点,点F,G,H分别是BC,BE,CE的中点.
(1)求证:△BGF≌△FHC;
(2)设AD=a,当四边形EGFH是正方形时,求矩形ABCD的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com