
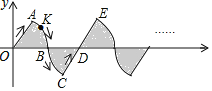
【题目】在平面直角坐标系xOy中,若干个半径为1个单位长度,圆心角是![]() 的扇形按图中的方式摆放,动点K从原点O出发,沿着“半径OA
的扇形按图中的方式摆放,动点K从原点O出发,沿着“半径OA![]() 弧AB
弧AB![]() 弧BC
弧BC![]() 半径CD
半径CD![]() 半径DE
半径DE![]() ”的曲线运动,若点K在线段上运动的速度为每秒1个单位长度,在弧线上运动的速度为每秒
”的曲线运动,若点K在线段上运动的速度为每秒1个单位长度,在弧线上运动的速度为每秒![]() 个单位长度,设第n秒运动到点K,
个单位长度,设第n秒运动到点K,![]() 为自然数
为自然数![]() ,则
,则![]() 的坐标是____,
的坐标是____,![]() 的坐标是____
的坐标是____
科目:初中数学 来源: 题型:
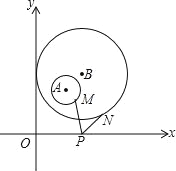
【题目】如图,平面直角坐标系中,分别以点A(2,3)、点B(3,4)为圆心,以1、3为半径作⊙A、⊙B,M,N分别是⊙A、⊙B上的动点,P为x轴上的动点,则PM+PN的最小值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
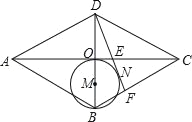
【题目】如图,在菱形ABCD中,对角线AC、BD交于点O,以OB为直径画圆M,过D作⊙M的切线,切点为N,分别交AC、BC于点E、F,已知AE=5,CE=3,则DF的长是( )
A. 3B. 4C. 4.8D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
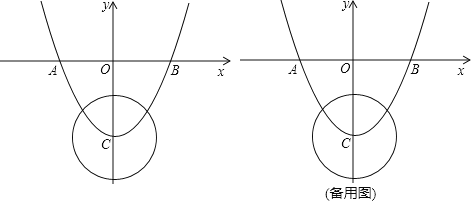
【题目】如图,已知二次函数![]() 的图象与x轴交于A,B两点,与y轴交于点C,
的图象与x轴交于A,B两点,与y轴交于点C,![]() 的半径为
的半径为![]() ,P为
,P为![]() 上一动点.
上一动点.
![]() 点B,C的坐标分别为
点B,C的坐标分别为![]() ______
______![]() ,
,![]() ______
______![]() ;
;
![]() 是否存在点P,使得
是否存在点P,使得![]() 为直角三角形?若存在,求出点P的坐标;若不存在,请说明理由;
为直角三角形?若存在,求出点P的坐标;若不存在,请说明理由;
![]() 连接PB,若E为PB的中点,连接OE,则OE的最大值
连接PB,若E为PB的中点,连接OE,则OE的最大值![]() ______.
______.
查看答案和解析>>
科目:初中数学 来源: 题型:
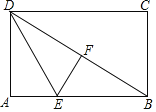
【题目】已知:如图,在矩形纸片ABCD中,![]() ,
,![]() ,翻折矩形纸片,使点A落在对角线DB上的点F处,折痕为DE,打开矩形纸片,并连接EF.
,翻折矩形纸片,使点A落在对角线DB上的点F处,折痕为DE,打开矩形纸片,并连接EF.
![]() 的长为多少;
的长为多少;
![]() 求AE的长;
求AE的长;
![]() 在BE上是否存在点P,使得
在BE上是否存在点P,使得![]() 的值最小?若存在,请你画出点P的位置,并求出这个最小值;若不存在,请说明理由.
的值最小?若存在,请你画出点P的位置,并求出这个最小值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某食品厂生产一种半成品食材,产量![]() 百千克
百千克![]() 与销售价格
与销售价格![]() 元
元![]() 千克
千克![]() 满足函数关系式
满足函数关系式![]() ,从市场反馈的信息发现,该半成品食材的市场需求量
,从市场反馈的信息发现,该半成品食材的市场需求量![]() 百千克
百千克![]() 与销售价格
与销售价格![]() 元
元![]() 千克
千克![]() 满足一次函数关系,如下表:
满足一次函数关系,如下表:
销售价格 | 2 | 4 |
| 10 |
市场需求量 | 12 | 10 |
| 4 |
已知按物价部门规定销售价格x不低于2元![]() 千克且不高于10元
千克且不高于10元![]() 千克
千克
![]() 求q与x的函数关系式;
求q与x的函数关系式;
![]() 当产量小于或等于市场需求量时,这种半成品食材能全部售出,求此时x的取值范围;
当产量小于或等于市场需求量时,这种半成品食材能全部售出,求此时x的取值范围;
![]() 当产量大于市场需求量时,只能售出符合市场需求量的半成品食材,剩余的食材由于保质期短而只能废弃
当产量大于市场需求量时,只能售出符合市场需求量的半成品食材,剩余的食材由于保质期短而只能废弃![]() 若该半成品食材的成本是2元
若该半成品食材的成本是2元![]() 千克.
千克.
![]() 求厂家获得的利润
求厂家获得的利润![]() 百元
百元![]() 与销售价格x的函数关系式;
与销售价格x的函数关系式;
![]() 当厂家获得的利润
当厂家获得的利润![]() 百元
百元![]() 随销售价格x的上涨而增加时,直接写出x的取值范围
随销售价格x的上涨而增加时,直接写出x的取值范围![]() 利润
利润![]() 售价
售价![]() 成本
成本![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】初三某班同学小戴想根据学习函数的经验,通过研究一个未学过的函数的图象,从而探究其各方面性质.
下表是函数y与自变量x的几组对应值:
x | … | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 9 | 12 | … |
y | … | -4 | 0 | 4 | 8 | 12 | 9 | 7.2 | 6 | 4 | 3 | … |
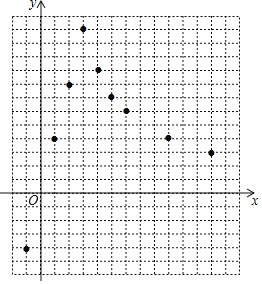
(1)在平面直角坐标系xOy中,每个小正方形的边长为一个单位长度,描出了以上表中各对对应值为坐标的点,请根据描出的点,画出该函数的图象.
(2)请根据画出的函数图象,直接写出该函数的关系式y=______(请写出自变量的取值范围),并写出该函数的一条性质:______.
(3)当直线y=-![]() x+b与该函数图象有3个交点时,求b的取值范围.
x+b与该函数图象有3个交点时,求b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD中,点E,F分别是边BC,AB上的点,且CE=BF.连接DE,过点E作EG⊥DE,使EG=DE,连接FG,FC.
(1)请判断:FG与CE的关系是___;
(2)如图2,若点E,F分别是边CB,BA延长线上的点,其它条件不变,(1)中结论是否仍然成立?请作出判断并给予证明;
(3)如图3,若点E,F分别是边BC,AB延长线上的点,其它条件不变,(1)中结论是否仍然成立?请直接写出你的判断.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,∠BAC=90°,AB=AC,点D是BC上一动点,连接AD,过点A作AE⊥AD,并且始终保持AE=AD,连接CE.
(1)求证:△ABD ≌△ACE ;
(2)若AF平分∠DAE交BC于F,探究线段BD,DF,FC之间的数量关系,并证明;
(3)在(2)的条件下,若BD=3,CF=4,求AD的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com