
【题目】如图,△ABC为等边三角形,点P为边BC上一点,在AC上取一点D,使AD=AP.
(1)若∠APD=80°,求∠DPC的度数;
(2)若∠APD=α,求∠BAP(用含α的式子表示).

【答案】(1)∠DPC=20°;(2)∠BAP=2α-120°.
【解析】
(1)在△APD中,求得∠PAD的度数,进而求得∠APC的度数,进而即可求解;
(2)由(1)解题思路和三角形的内角和定理即可求出∠BAP的度数.
(1)在△APD中,AP=AD,
∴∠APD=∠ADP=80°
∴∠PAD=180°-80°-80°=20°
∴∠BAP=60°-20°=40°
∴∠APC=∠B+∠BAP=60°+40°=100°
∴∠DPC=∠APC-∠APD=100°-80°=20°.
(2)∵在△APD中,AP=AD,
∴∠APD=∠ADP=α°
∴∠PAD=180°-α°-α°=180°-2α°
∴∠BAP=60°-(180°-2α°)=(2α-120)°.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
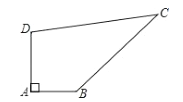
【题目】已知某开发区有一块四边形的空地![]() ,如图所示,现计划在空地上种植草皮,经测量
,如图所示,现计划在空地上种植草皮,经测量![]() ,AB=3m,BC=12m,CD=13m,DA=4m,若每平方米草皮需要200元,问要多少投入?
,AB=3m,BC=12m,CD=13m,DA=4m,若每平方米草皮需要200元,问要多少投入?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别为E,F,则下列四个结论:①AD上任意一点到点C,B的距离相等;②AD上任意一点到AB,AC的距离相等;③BD=CD,AD⊥BC;④∠BDE=∠CDF.其中正确的个数是( )
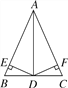
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
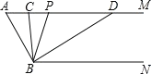
【题目】如图,已知AM∥BN,∠A=80°,点P是射线AM上的动点(与A不重合),BC、BD分别平分∠ABP和∠PBN,交射线AM于点C、D.
(1)求∠CBD的度数;
(2)当点P运动时,∠APB∶∠ADB的度数比值是否随之发生变化?若不变,请求出这个比值;若变化,请找出变化规律.
(3)当点P运动到使∠ACB=∠ABD时,求∠ABC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,D是AB边上一点,以CD为边作等边△CDE,使点E、A在直线DC的同侧,连接AE,判断AE与BC的位置关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AB=9,AD=6,∠ADC的平分线交AB于点E,交CB的延长线于点F,AG⊥DE,垂足为G.若AG=4 ![]() ,则△BEF的面积是( )
,则△BEF的面积是( )
A.![]()
B.2 ![]()
C.3 ![]()
D.4 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为4,点E在BC上,四边形EFGB也是正方形,以B为圆心,BA长为半径画 ![]() ,连结AF,CF,则图中阴影部分面积为 .
,连结AF,CF,则图中阴影部分面积为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张老师利用休息时间组织学生测量山坡上一棵大树CD的高度,如图,山坡与水平面成30°角(即∠MAN=30°),在山坡底部A处测得大树顶端点C的仰角为45°,沿坡面前进20米,到达B处,又测得树顶端点C的仰角为60°(图中各点均在同一平面内),求这棵大树CD的高度(结果精确到0.1米,参考数据: ![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中学生上学带手机的现象越来越受到社会的关注,为此媒体记者随机调查了某校若干名学生上学带手机的目的,分为四种类型:A接听电话;B收发短信;C查阅资料;D游戏聊天.并将调查结果绘制成图1和图2的统计图(不完整),请根据图中提供的信息,解答下列问题: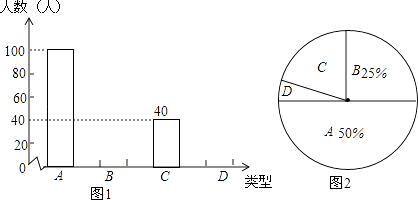
(1)此次抽样调查中,共调查了名学生;
(2)将图1、图2补充完整;
(3)现有4名学生,其中A类两名,B类两名,从中任选2名学生,求这两名学生为同一类型的概率(用列表法或树状图法).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com