
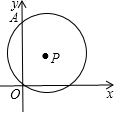
 如图,点P(1,2),⊙P经过原点O,交y轴正半轴于点A,点B在⊙P上,∠BAO=45°,则点B的坐标是(3,1)或(-1,3).
如图,点P(1,2),⊙P经过原点O,交y轴正半轴于点A,点B在⊙P上,∠BAO=45°,则点B的坐标是(3,1)或(-1,3). 分析 作辅助线,先利用勾股定理求圆P的半径为$\sqrt{5}$,根据已知中的∠BAO=45°可知,两个满足条件的点B的连线就是圆P的直径,由此证明△B1OG≌△B2OH,设B1(x,y),则OG=x,B1G=y,从而列方程组可求出x、y的值,写出符合条件的点B的坐标.
解答 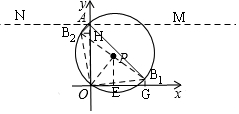 解:连接OP,过P作PE⊥x轴于E,
解:连接OP,过P作PE⊥x轴于E,
∵P(1,2),
∴OE=1,PE=2,
由勾股定理得:OP=$\sqrt{{2}^{2}+{1}^{2}}$=$\sqrt{5}$,
过A作MN⊥y轴,分别作∠MAO、∠NAO的平分线交⊙P于B1、B2,
则∠B1AO=45°,∠B2AO=45°,
∴∠B2AB1=90°,
连接B1B2,则B1B2是⊙P的直径,即过点P,
∴B1B2=2$\sqrt{5}$,
∴∠B2OB1=90°,
∵∠OB2B1=∠B1AO=45°,
∴△B1B2O是等腰直角三角形,
∴OB1=OB2=$\frac{2\sqrt{5}}{\sqrt{2}}$=$\sqrt{10}$,
过B1作B1G⊥x轴于G,过B2作B2H⊥y轴于H,
∴∠OGB1=∠OHB2=90°,
∵∠GOB1+∠AOB1=90°,∠B2OH+∠AOB1=90°,
∴∠GOB1=∠B2OH,
∴△B1OG≌△B2OH,
∴B1G=B2H,OG=OH,
设B1(x,y),则OG=x,B1G=y,
∵∠B2AO=45°,
∴△AB2H是等腰直角三角形,
∴B2H=AH=B1G=y,
∴AO=AH+OH=x+y=4,
则$\left\{\begin{array}{l}{x+y=4}\\{{x}^{2}+{y}^{2}=(\sqrt{10})^{2}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{x}_{1}=3}\\{{y}_{1}=1}\end{array}\right.$ $\left\{\begin{array}{l}{{x}_{2}=1}\\{{y}_{2}=3}\end{array}\right.$,
∵PB=$\sqrt{5}$,
∴x=1,y=3不符合题意,舍去,
∴B1(3,1),B2(-1,3),
则点B的坐标为(3,1)或(-1,3),
故答案为:(3,1)或(-1,3).
点评 本题考查了圆周角定理、坐标与图形的性质,熟练掌握圆周角的相关定理是关键,注意确定满足条件的点B,作辅助线,构建全等三角形和等腰直角三角形,从而解决问题.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:填空题
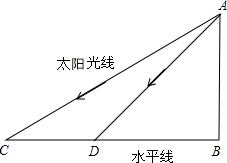 在同一时刻太阳光线与水平线的夹角是一定的.如图,有一垂直于地面的物体AB.在某一时刻太阳光线与水平线的夹角为30°时,物体AB的影长BC为4米;在另一个时刻太阳光线与水平线的夹角为45°时,则物体AB的影长BD为$\frac{4\sqrt{3}}{3}$米.(结果保留根号)
在同一时刻太阳光线与水平线的夹角是一定的.如图,有一垂直于地面的物体AB.在某一时刻太阳光线与水平线的夹角为30°时,物体AB的影长BC为4米;在另一个时刻太阳光线与水平线的夹角为45°时,则物体AB的影长BD为$\frac{4\sqrt{3}}{3}$米.(结果保留根号)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 小亮 | B. | 小丽 | C. | 小红 | D. | 小强 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com