
【题目】如图,△ABC是等边三角形,四边形BDEF是菱形,其中线段DF的长与DB相等,将菱形BDEF绕点B按顺时针方向旋转,甲、乙两位同学发现在此旋转过程中,有如下结论.
甲:线段AF与线段CD的长度总相等;
乙:直线AF和直线CD所夹的锐角的度数不变.
那么,你认为( )

A. 甲、乙都对 B. 乙对甲不对 C. 甲对乙不对 D. 甲、乙都不对
【答案】A
【解析】
连接DF、AF、CD(如图),证明△BDF为等边三角形,即可得∠DBF=60°,再证明△ABF绕点B顺时针旋转60°可得到△CBD,即可得AF=CD,∠FAB=∠DCB,甲的说法正确;因为∠FAB+∠AMN+∠ANM=∠DCB+∠ABC+∠BNC=180°,∠ANM=∠BNC,即可得∠AMN=∠ABC=60°,乙的说法正确.
连接DF、AF、CD,如图,
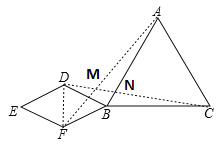
四边形BDEF为菱形,
∴BD=BF,
∵DF=BD,
∴BD=BF=DF,
∴△BDF为等边三角形,
∴∠DBF=60°,
∵△ABC为等边三角形,
∴BA=BC,∠ABC=60°,
∴∠ABF=∠CBD,
∴△ABF绕点B顺时针旋转60°可得到△CBD,
∴AF=CD,∠FAB=∠DCB,
∴∠FAB+∠AMN+∠ANM=∠DCB+∠ABC+∠BNC=180°,
∵∠ANM=∠BNC,
∴∠AMN=∠ABC=60°,
即直线AF和直线CD所夹的锐角的度数为60°.
综上,甲、乙的结论都对.
故选A.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
【题目】阅读材料1:
对于两个正实数![]() ,由于
,由于![]() ,所以
,所以![]() ,即
,即![]() ,所以得到
,所以得到![]() ,并且当
,并且当![]() 时,
时,![]()
阅读材料2:
若![]() ,则
,则![]() ,因为
,因为![]() ,
,![]() ,所以由阅读材料1可得:
,所以由阅读材料1可得:![]() ,即
,即![]() 的最小值是2,只有
的最小值是2,只有![]() 时,即
时,即![]() =1时取得最小值.
=1时取得最小值.
根据以上阅读材料,请回答以下问题:
(1)比较大小
![]()
![]() (其中
(其中![]() ≥1);
≥1); ![]() -2(其中
-2(其中![]() <-1)
<-1)
(2)已知代数式![]() 变形为
变形为![]() ,求常数
,求常数![]() 的值
的值
(3)当![]() = 时,
= 时,![]() 有最小值,最小值为 (直接写出答案).
有最小值,最小值为 (直接写出答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,射线OM在第一象限,且与x轴正半轴的夹角为60°,过点D(6,0)作DA⊥OM于点A,作线段 OD的垂直平分线BE交x轴于点E,交AD于点B,作射线OB.以AB为边在△AOB的外侧作正方形ABCA1,延长A1C交射线OB于点B1,以A1B1为边在△A1OB1的外侧作正方形A1B1C1A2,延长A2C1交射线OB于点B2,以A2B2为边在△A2OB2的外侧作正方形A2B2C2A3……按此规律进行下去,则正方形A2017B2017C2017A2018的周长为______________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,以□ABCD的较短边CD为一边作菱形CDEF,使点F落在边AD上,连接BE,交AF于点G.
(1)猜想BG与EG的数量关系.并说明理由;
(2)延长DE,BA交于点H,其他条件不变,
①如图2,若∠ADC=60°,求![]() 的值;
的值;
②如图3,若∠ADC=α(0°<α<90°),直接写出![]() 的值.(用含α的三角函数表示)
的值.(用含α的三角函数表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=4,∠ABC和∠ACB的平分线交于点E,过点E作MN∥BC分别交AB、AC于M、N,则△AMN的周长为______________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,∠BAC=50°,P是BC边上一点,将△ABP绕点A逆时针旋转50°,点P旋转后的对应点为点P′.
(1)画出旋转后的三角形;
(2)连接PP′,若∠BAP=20°,求∠PP′C的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,MN表示某引水工程的一段设计路线,从点M到点N的走向为北偏西30°,在点M的北偏西60°方向上有一点A,以点A为圆心,以500米为半径的圆形区域为居民区,取MN上另一点B,测得BA的方向为北偏西75°.已知MB=400米,若不改变方向,则输水路线是否会穿过居民区?请通过计算说明理由.(参考数据: ![]() ≈1.732)
≈1.732)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】河西中学九年级共有9个班,300名学生,学校要对该年级学生数学学科学业水平测试成绩进行抽样分析,请按要求回答下列问题:
(1)(收集数据)若从所有成绩中抽取一个容量为36的样本,以下抽样方法中最合理的是________.
①在九年级学生中随机抽取36名学生的成绩;
②按男、女各随机抽取18名学生的成绩;
③按班级在每个班各随机抽取4名学生的成绩.
(2)(整理数据)将抽取的36名学生的成绩进行分组,绘制频数分布表和成绩分布扇形统计图如下.请根据图表中数据填空:
成绩(单位:分) | 频数 | 频率 |
A类(80~100) | 18 |
|
B类(60~79) | 9 |
|
C类(40~59) | 6 |
|
D类(0~39) | 3 |
|
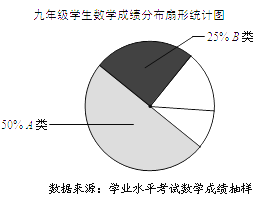
①C类和D类部分的圆心角度数分别为________°、________°;
②估计九年级A、B类学生一共有________名.
(3)(分析数据)教育主管部门为了解学校教学情况,将河西、复兴两所中学的抽样数据进行对比,得下表:
学校 | 平均数(分) | 极差(分) | 方差 | A、B类的频率和 |
河西中学 | 71 | 52 | 432 | 0.75 |
复兴中学 | 71 | 80 | 497 | 0.82 |
你认为哪所学校本次测试成绩较好,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com