练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    16．在一个密闭不透明的袋子里有若干个白球．为估计白球个数，小何向其中投入8个黑球，搅拌均匀后随机摸出一个球，记下颜色，再把它放入袋中，不断重复摸球400次，其中88次摸到黑球，则估计袋中大约有白球（　　）
    A．18个B．28个C．36个D．42个

    分析 根据摸到黑球的概率和黑球的个数，可以求出袋中放入黑球后总的个数，然后再减去黑球个数，即可得到白球的个数．

    解答 解：由题意可得，
    白球的个数大约为：8÷$\frac{88}{400}$-8≈28，
    故选B．

    点评 本题考查用样本估计总体，解题的关键是明确题意，根据摸到黑球的概率求出总体．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    11．如图是由4个完全相同的小正方体组成的立体图形，则它的俯视图是（　　）
    A．B．C．D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．一般情况下，学生注意力上课后逐渐增强，中间有段时间处于较理想的稳定状态，随后开始分散．实验结果表明，学生注意力指数y随时间x（min）的变化规律如图所示（其中AB、BC分别为线段，CD为双曲线的一部分）：
    （1）上课后第5min与第30min相比较，何时学生注意力更集中？
    （2）某道难题需连续讲19min，为保证效果，学生注意力指数不宜低于36，老师能否在所需要求下讲完这道题？

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    4．反比例函数y=$\frac{k-1}{x}$的图象经过A（x1，y1），B（x2，y2）两点，其中x1＜x2＜0，且y1＞y2，则k的范围是k＞1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

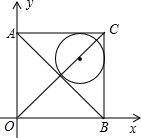    11．如图，在平面直角坐标系中有一正方形AOBC，反比例函数y=$\frac{k}{x}$经过正方形AOBC对角线的交点，半径为4-2$\sqrt{2}$的圆内切于△ABC，则k的值为（　　）
    A．$\sqrt{2}$B．2C．4D．2$\sqrt{2}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    1．如图，已知点B，D在反比例函数y=$\frac{a}{x}$（a＞0）的图象上，点A，C在反比例函数y=$\frac{b}{x}$（b＜0）的图象上，AB∥CD∥x轴，AB，CD在x轴的同侧，AB=4，CD=3，AB与CD的距离为1，则a-b的值是12．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    8．关于反比例函数y=-$\frac{4}{x}$，下列说法正确的是（　　）
    A．图象在第一、三象限B．图象经过点（2，-8）
    C．当x＞0时，y随x的增大而减小D．当x＜0时，y随x的增大而增大

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．如图，抛物线y=ax2+bx+c（a≠0）与x轴交于点A（-1，0）、B（3，0），交于点C（0，-3），设该抛物线的顶点坐标为D，连接AC．

    （1）求抛物线的解析式及顶点D的坐标；
    （2）在抛物线的对称轴上存在一点P，使△PAC的周长最小，请求出点P的坐标；
    （3）在抛物线上是否存在一点M，使S△MAC=2S△BCD？若存在，求出点M的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

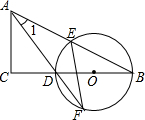    6．如图，在△ABC中，∠C=90°，D是BC边上一点，以DB为直径的⊙O经过AB的中点E，交AD的延长线于点F，连结EF．
    （1）求证：∠1=∠F．
    （2）若sinB=$\frac{\sqrt{5}}{5}$，EF=2$\sqrt{5}$，求CD的长．

    查看答案和解析>>

    同步练习册答案