
【题目】在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 、
、![]() 分别在射线
分别在射线![]() 、
、![]() 上(点
上(点![]() 不与点
不与点![]() 、点
、点![]() 重合),且保持
重合),且保持![]() .
.
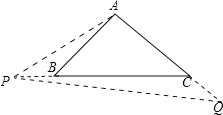
①若点![]() 在线段
在线段![]() 上(如图),且
上(如图),且![]() ,求线段
,求线段![]() 的长;
的长;
②若![]() ,
,![]() ,求
,求![]() 与
与![]() 之间的函数关系式,并写出自变量的取值范围;
之间的函数关系式,并写出自变量的取值范围;

【答案】(1)、CQ=2.4;(2)、![]() ,(0<x<8);
,(0<x<8);![]() (x≥8)
(x≥8)
【解析】
试题分析:(1)、根据∠APQ+∠CPQ=∠B+∠BAP,∠APQ=∠ABC得出∠BAP=∠CQP,然后得到△CPQ∽△BAP,根据相似比得出CQ的长度;(2)、若点P在线段CB上,根据第一题的相似比得出函数解析式;若点P在线段CB的延长线上,根据同样的方法证明△QCP∽△PBA,然后根据相似比得出函数解析式.
试题解析:(1)、∵∠APQ+∠CPQ=∠B+∠BAP,∠APQ=∠ABC,∴∠BAP=∠CQP.又∵AB=AC,∴∠B=∠C.
∴△CPQ∽△BAP.∴![]() .∵AB=AC=5,BC=8,BP=6,CP=8﹣6=2,∴
.∵AB=AC=5,BC=8,BP=6,CP=8﹣6=2,∴![]() ,
,![]() .
.
(2)、若点P在线段CB上,由(1)知![]() ,∵BP=x,BC=8,∴CP=BC﹣BP=8﹣x,
,∵BP=x,BC=8,∴CP=BC﹣BP=8﹣x,
又∵CQ=y,AB=5,∴![]() ,即
,即![]() .故所求的函数关系式为
.故所求的函数关系式为![]() ,(0<x<8).
,(0<x<8).
若点P在线段CB的延长线上,如图.∵∠APQ=∠APB+∠CPQ,∠ABC=∠APB+∠PAB,∠APQ=∠ABC,
∴∠CPQ=∠PAB.又∵∠ABP=180°﹣∠ABC,∠PCQ=180°﹣∠ACB,∠ABC=∠ACB,
∴∠ABP=∠PCQ.∴△QCP∽△PBA.∴![]() .∵BP=x,CP=BC+BP=8+x,AB=5,CQ=y,
.∵BP=x,CP=BC+BP=8+x,AB=5,CQ=y,
∴![]() ,即
,即![]() (x≥8)
(x≥8)


科目:初中数学 来源: 题型:
【题目】如图,△ABC和△DEF均是边长为4的等边三角形,△DEF的顶点D为△ABC的一边BC的中点,△DEF绕点D旋转,且边DF、DE始终分别交△ABC的边AB、AC于点H、G,图中直线BC两侧的图形关于直线BC成轴对称.连结HH′、HG、GG′、H′G′,其中HH′、GG′分别交BC于点I、J.
(1)求证:△DHB∽△GDC;
(2)设CG=x,四边形HH′G′G的面积为y,
①求y关于x的函数解析式和自变量x的取值范围.
②求当x为何值时,y的值最大,最大值为多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,现有甲、乙两个小分队分别同时从B、C两地出发前往A地,甲沿线路BA行进,乙沿线路CA行进,已知C在A的南偏东55°方向,AB的坡度为1:5,同时由于地震原因造成BC路段泥石堵塞,在BC路段中位于A的正南方向上有一清障处H,负责抢修BC路段,已知BH为12000m.
(1)求BC的长度;
(2)如果两个分队在前往A地时匀速前行,且甲的速度是乙的速度的三倍.试判断哪个分队先到达A地.(tan55°≈1.4,sin55°≈0.84,cos55°≈0.6,![]() ≈5.01,结果保留整数)
≈5.01,结果保留整数)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一方有难八方支援,某市政府筹集了抗旱必需物资120吨打算运往灾区,现有甲、乙、丙三种车型供选择,每辆车的运载能力和运费如下表所示:(假设每辆车均满载)
车型 | 甲 | 乙 | 丙 |
汽车运载量(吨/辆) | 5 | 8 | 10 |
汽车运费(元/辆) | 400 | 500 | 600 |
(1)若全部物资都用甲、乙两种车型来运送,需运费8200元,问分别需甲、乙两种车型各几辆?
(2)为了节约运费,该市政府可以调用甲、乙、丙三种车型参与运送,已知它们的总辆数为16辆,你能通过列方程组的方法分别求出几种车型的辆数吗?
(3)求出那种方案的运费最省?最省是多少元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一名射击爱好者7次射击的中靶环数如下(单位:环):7,10,9,8,7,9,9,这7个数据的中位数是( )
A.7环B.8环C.9环D.10环
查看答案和解析>>
科目:初中数学 来源: 题型:
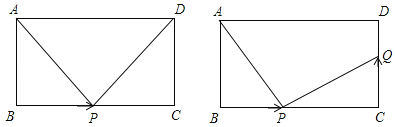
【题目】如图,在长方形ABCD中,AB=CD=6cm,BC=10cm,点P从点B出发,以2cm/秒的速度沿BC向点C运动,设点P的运动时间为t秒:
(1)PC=______cm.(用t的代数式表示)
(2)当t为何值时,△ABP≌△DCP?
(3)当点P从点B开始运动,同时,点Q从点C出发,以v cm/秒的速度沿CD向点D运动,是否存在这样v的值,使得△ABP与△PQC全等?若存在,请求出v的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com