
计算:  -
- ÷
÷ =__________.
=__________.
科目:初中数学 来源:2017-2018学年黑龙江省哈尔滨市双城区七年级(上)期末数学试卷(五四学制) 题型:单选题
为确保信息安全,信息需要加密传输,发送方由明文→密文(解密).接收方由密文→明文(解密)。已知加密规则为:明文a,b,c对应的密文a+1,2b+4,3c+9,例如明文1,2,3对应的密文2,8,18。如果接收方收到密文7,18,15,则解密得到的明文为( )
A. 4,5,6 B. 6,7,2 C. 2,6,7 D. 7,2,6
B 【解析】试题分析:首先根据必须理解密文的加密方法,然后进行计算.根据题意得:a+1=7,2b+4=18,3c+9=15 则a=6,b=7,c=2,即明文为6,7,2.查看答案和解析>>
科目:初中数学 来源:2017-2018学年九年级数学北师大版上册 第3章 概率的进一步认识 单元测试卷 题型:填空题
从甲、乙、丙、丁4名三好学生中随机抽取2名学生担任升旗手,则抽取的2名学生是甲和乙的概率为 ________.
【解析】试题分析:随机抽取的所有可能情况为:甲乙;甲丙;甲丁;乙丙;乙丁;丙丁六种情况,则符合条件的只有一种情况,则P(抽取的2名学生是甲和乙)=1÷6=.查看答案和解析>>
科目:初中数学 来源:2017-2018学年八年级数学人教版上册 全册综合测试卷 题型:解答题
如图①,CA=CB,CD=CE,∠ACB=∠DCE=α,AD,BE相交于点M,连接CM.
(1)求证:BE=AD;
(2)用含α的式子表示∠AMB的度数;
(3)当α=90°时,取AD,BE的中点分别为点P,Q,连接CP,CQ,PQ,如图②,判断△CPQ的形状,并加以证明.

查看答案和解析>>
科目:初中数学 来源:2017-2018学年八年级数学人教版上册 全册综合测试卷 题型:填空题
如图,△ABC是等边三角形,AE=CD,AD、BE相交于点P,BQ⊥DA于Q,PQ=3,EP=1,则DA的长是________.

查看答案和解析>>
科目:初中数学 来源:2017-2018学年八年级数学人教版上册 全册综合测试卷 题型:单选题
如图,点B、F、C、E在一条直线上,AB∥ED,AC∥FD,那么添加下列一个条件后,仍无法判定△ABC≌△DEF的是( )

A. AB=DE B. AC=DF C. ∠A=∠D D. BF=EC
C 【解析】试题分析:【解析】 选项A、添加AB=DE可用AAS进行判定,故本选项错误; 选项B、添加AC=DF可用AAS进行判定,故本选项错误; 选项C、添加∠A=∠D不能判定△ABC≌△DEF,故本选项正确; 选项D、添加BF=EC可得出BC=EF,然后可用ASA进行判定,故本选项错误. 故选C.查看答案和解析>>
科目:初中数学 来源:2017-2018学年八年级数学人教版上册 全册综合测试卷 题型:单选题
已知2m+3n=5,则4m·8n=( )
A. 16 B. 25 C. 32 D. 64
C 【解析】∵, ∴. 故选C.查看答案和解析>>
科目:初中数学 来源:湖南邵阳市区2017-2018学年八年级上册数学期末试卷 题型:单选题
甲、乙两人同时从A地出发,骑自行车行30千米到B地,甲比乙每小时少走3千米,结果乙先到40分钟。若设乙每小时走x千米,则可列方程( )
A.  B.
B. 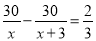 C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源:湖北省襄阳老河口市2018届九年级上学期期末考试数学试卷 题型:填空题
如图,在Rt△ABC中,∠C=90°,∠BAC=60°,BC= ,将△ABC绕点A逆时针旋转60°后得到△ADE,则线段BC在上述旋转过程中所扫过部分(阴影部分)的面积是__________(结果保留π).
,将△ABC绕点A逆时针旋转60°后得到△ADE,则线段BC在上述旋转过程中所扫过部分(阴影部分)的面积是__________(结果保留π).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com