
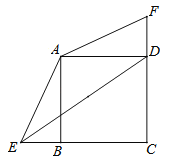
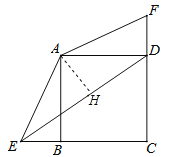
【题目】已知正方形ABCD中,BC=3,点E、F分别是CB、CD延长线上的点,DF=BE,连接AE、AF,过点A作AH⊥ED于H点.
(1)求证:△ADF≌△ABE;
(2)若BE=1,求tan∠AED的值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)根据辅助线的性质得到AD=AB,∠ADC=∠ABC=90°,由邻补角的定义得到∠ADF=∠ABE=90°,于是得到结论;
(2)过点A作AH⊥DE于点H,根据勾股定理得到AE=![]() ,ED=
,ED=![]() =5,根据三角形的面积S△AED=
=5,根据三角形的面积S△AED=![]() AD×BA=
AD×BA=![]() ,S△ADE=
,S△ADE=![]() ED×AH=
ED×AH=![]() ,求得AH=1.8,由三角函数的定义即可得到结论.
,求得AH=1.8,由三角函数的定义即可得到结论.
试题解析:(1)正方形ABCD中,∵AD=AB,∠ADC=∠ABC=90°,∴∠ADF=∠ABE=90°,在△ADF与△ABE中,∵AD=AB,∠ADF=∠ABE,DF=BE,∴△ADF≌△ABE;
(2)过点A作AH⊥DE于点H,在Rt△ABE中,∵AB=BC=3,∵BE=1,∴AE=![]() ,ED=
,ED=![]() =5,∵S△AED=
=5,∵S△AED=![]() AD×BA=
AD×BA=![]() ,S△ADE=
,S△ADE=![]() ED×AH=
ED×AH=![]() ,解出AH=1.8,在Rt△AHE中,EH=2.6,∴tan∠AED=
,解出AH=1.8,在Rt△AHE中,EH=2.6,∴tan∠AED=![]() =
=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
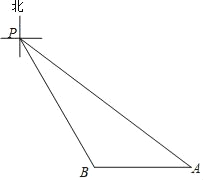
【题目】如图,P点是某海域内的一座灯塔的位置,船A停泊在灯塔P的南偏东53°方向的50海里处,船B位于船A的正西方向且与灯塔P相距20![]() 海里.(本题参考数据sin53°≈0.80,cos53°≈0.60,tan53°≈1.33.)
海里.(本题参考数据sin53°≈0.80,cos53°≈0.60,tan53°≈1.33.)
(1)试问船B在灯塔P的什么方向?
(2)求两船相距多少海里?(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD和矩形EFGO在平面直角坐标系中,点B,F的坐标分别为(-4,4),(2,1).若矩形ABCD和矩形EFGO是位似图形,点P(点P在GC上)是位似中心,则点P的坐标为( )
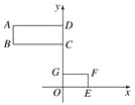
A. (0,3)
B. (0,2.5)
C. (0,2)
D. (0,1.5)
查看答案和解析>>
科目:初中数学 来源: 题型:
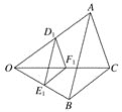
【题目】如图,O点是△ABC与△D1E1F1的位似中心,△ABC的周长为1.若D1、E1、F1分别是线段OA、OB、OC的中点,则△D1E1F1的周长为![]() ;若OD2=
;若OD2=![]() OA、OE2=
OA、OE2=![]() OB、OF2=
OB、OF2=![]() OC,则△D2E2F2的周长为
OC,则△D2E2F2的周长为![]() ;…若ODn=
;…若ODn=![]() OA、OEn=
OA、OEn=![]() OB、OFn=
OB、OFn=![]() OC,则△DnEnFn的周长为__________.(用正整数n表示)
OC,则△DnEnFn的周长为__________.(用正整数n表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 的正方形方格中,每个小正方形的边长都为1,顶点都在网格线交点处的三角形,
的正方形方格中,每个小正方形的边长都为1,顶点都在网格线交点处的三角形, ![]() 是一个格点三角形.
是一个格点三角形.
![]() 在图
在图![]() 中,请判断
中,请判断![]() 与
与![]() 是否相似,并说明理由;
是否相似,并说明理由;
![]() 在图
在图![]() 中,以O为位似中心,再画一个格点三角形,使它与
中,以O为位似中心,再画一个格点三角形,使它与![]() 的位似比为2:1
的位似比为2:1
![]() 在图
在图![]() 中,请画出所有满足条件的格点三角形,它与
中,请画出所有满足条件的格点三角形,它与![]() 相似,且有一条公共边和一个公共角.
相似,且有一条公共边和一个公共角.

查看答案和解析>>
科目:初中数学 来源: 题型:
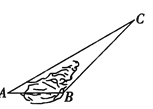
【题目】如图,A,B两地之间有一座山,汽车原来从A地到B地需经C地沿折线ACB行驶,现开通隧道后,汽车直接沿直线AB行驶即可到达B地.已知AC=120km,∠A=30°,∠B=135°,求隧道开通后汽车从A地到B地需行驶多少千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,□ABCD的对角线相交于点O,点E在边BC的延长线上,且OE=OB,连接DE.

(1)求证:DE⊥BE;
(2)如果OE⊥CD,求证:BD·CE=CD·DE.
查看答案和解析>>
科目:初中数学 来源: 题型:
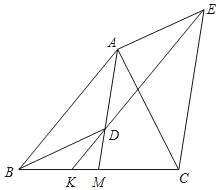
【题目】如图,AM是△ABC的中线,点D是线段AM上一点(不与点A重合).过点D作KD∥AB,交BC于点K,过点C作CE∥AM,交KD的延长线于点E,连接AE、BD.
(1)求证:△ABM∽△EKC;
(2)求证:ABCK=EKCM;
(3)判断线段BD、AE的关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com