【题目】填写下列空格完成证明：如图， EF∥AD ， 1 2 ， BAC 70 ，求AGD ．
解：∵ EF∥AD ，
∴ 2 ．（ ）
∵ 1 2 ，
∴ 1 3．（ ）
∴ ∥ ．（ ）
∴ BAC 180 ．（ ）
∵ BAC 70 ，
∴ AGD ．
【答案】∠3 ；两直线平行，同位角相等；等量代换；DG∥AB ；内错角相等，两直线平行；∠AGD ；两直线平行，同旁内角互补；110．
【解析】
此题要注意由EF∥AD，可得∠2=∠3，由等量代换可得∠1=∠3，可得DG∥BA，根据平行线的性质可得∠BAC+∠AGD=180°，即可求解．
∵EF=AD，
∴∠2=∠3，（两直线平行，同位角相等）
∵∠1=∠2，
∴∠1=∠3，（等量代换）
∴DG∥AB（内错角相等，两直线平行）
∴∠BAC+∠AGD=180°（两直线平行，同旁内角互补）
∵∠BAC=70°，
∴∠AGD=110°．
故答案为：∠3；两直线平行，同位角相等；等量代换；DG；AB；内错角相等，两直线平行；∠AGD；两直线平行，同旁内角互补；110．
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，一次函数y1=kx+b的图象分别交x轴，y轴于A、B两点，与反比例函数y2= 
的图象交于C、D两点，已知点C的坐标为（﹣4，﹣1），点D的横坐标为2．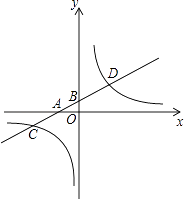
（1）求反比例函数与一次函数的解析式；
（2）直接写出当x为何值时，y1＞y2？
（3）点P是反比例函数在第一象限的图象上的点，且点P的横坐标大于2，过点P做x轴的垂线，垂足为点E，当△APE的面积为3时，求点P的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，小明坐在堤边A处垂钓，河堤AC与水平面的夹角为30°，AC的长为 
米，钓竿AO与水平线的夹角为60°，其长为3米，若AO与钓鱼线OB的夹角为60°，求浮漂B与河堤下端C之间的距离．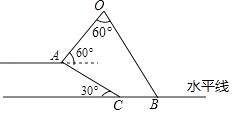
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ABC是等腰直角三角形，∠C=90°，点D是AB的中点，点E，F分别在BC，AC上，且AF=CE．
（1）填空：∠A的度数是 ．
（2）探究DE与DF的关系，并给出证明．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，点P是菱形ABCD的对角线AC上的一个动点，过点P垂直于AC的直线交菱形ABCD的边于M，N两点．设AC=2，BD=1，AP=x，△CMN的面积为y，则y关于x的函数图象大致形状是（ ）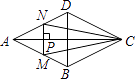
A.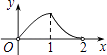
B.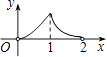
C.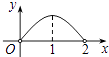
D.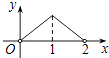
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】星期天，小明从家里出发到图书馆去看书，再回到家．他离家的距离y(千米)与时间t(分钟)的关系如图所示．
根据图像回答下列问题：
(1)小明家离图书馆的距离是________千米；
(2)小明在图书馆看书的时间为________小时；
(3)小明去图书馆时的速度是________千米/小时．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，某校数学兴趣小组为测得大厦AB的高度，在大厦前的平地上选择一点C，测得大厦顶端A的仰角为30°，再向大厦方向前进80米，到达点D处（C，D，B三点在同一直线上），又测得大厦顶端A的仰角为45°，请你计算该大厦的高度．（精确到0.1米，参考数据： 
≈1.414， 
≈1.732）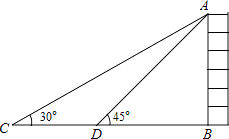
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系中，点A（a，0），点B（2﹣a，0），且A在B的左边，点C（1，﹣1），连接AC，BC，若在AB，BC，AC所围成区域内（含边界），横坐标和纵坐标都为整数的点的个数为4个，那么a的取值范围为（ ）
A. ﹣1＜a≤0B. 0≤a＜1C. ﹣1＜a＜1D. ﹣2＜a＜2
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】完成下列证明：
如图，已知AD⊥BC，EF⊥BC，∠1=∠2．
求证：DG∥BA．
证明：∵AD⊥BC，EF⊥BC（已知）
∴∠EFB=∠ADB=90°（ ）
∴EF∥AD（ ）
∴∠1=∠BAD（ ）
又∵∠1=∠2（已知）
∴ （等量代换）
∴DG∥BA．（ ）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com