
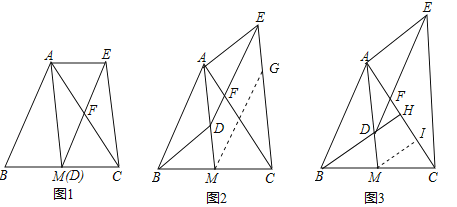
【题目】如图,AM是△ABC的中线,D是线段AM上一点(不与点A重合)DE∥AB交AC于点F,CE∥AM,连结AE.
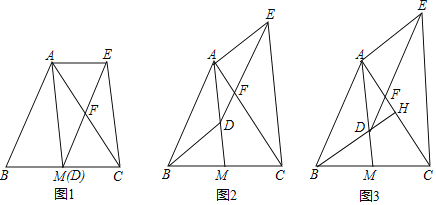
(1)如图1,当点D与M重合时,求证:四边形ABDE是平行四边形;
(2)如图2,当点D不与M重合时,(1)中的结论还成立吗?请说明理由.
(3)如图3,延长BD交AC于点H,若BH⊥AC,且BH=AM
①求∠CAM的度数;
②当FH=![]() , DM=4时,求DH的长.
, DM=4时,求DH的长.
【答案】(1)证明见解析;(2)证明见解析;(3)见解析.
【解析】试题分析:(1)只要证明AE=BM,AE∥BM即可解决问题;
(2)成立.如图2中,过点M作MG∥DE交CE于G.由四边形DMGE是平行四边形,推出ED=GM,且ED∥GM,由(1)可知AB=GM,AB∥GM,可知AB∥DE,AB=DE,即可推出四边形ABDE是平行四边形;
(3)①如图3中,取线段HC的中点I,连接MI,只要证明MI=![]() AM,MI⊥AC,即可解决问题;
AM,MI⊥AC,即可解决问题;
②设DH=x,则AH=![]() x,AD=2x,推出AM=4+2x,BH=4+2x,由四边形ABDE是平行四边形,推出DF∥AB,推出
x,AD=2x,推出AM=4+2x,BH=4+2x,由四边形ABDE是平行四边形,推出DF∥AB,推出![]() ,可得
,可得![]() ,解方程即可;
,解方程即可;
试题解析:(1)如图1中,∵DE∥AB,∴∠EDC=∠ABM,
∵CE∥AM,∴∠ECD=∠ADB,
∵AM是△ABC的中线,且D与M重合,∴BD=DC,∴△ABD≌△EDC,
∴AB=ED,∵AB∥ED,∴四边形ABDE是平行四边形.
(2)结论:成立.理由如下:
如图2中,过点M作MG∥DE交CE于G.
∵CE∥AM,∴四边形DMGE是平行四边形,∴ED=GM,且ED∥GM,
由(1)可知AB=GM,AB∥GM,∴AB∥DE,AB=DE,∴四边形ABDE是平行四边形;
(3)①如图3中,取线段HC的中点I,连接MI,
∵BM=MC,∴MI是△BHC的中位线,∴MI∥BH,MI=![]() BH,
BH,
∵BH⊥AC,且BH=AM,∴MI=![]() AM,MI⊥AC,∴∠CAM=30°.
AM,MI⊥AC,∴∠CAM=30°.
②设DH=x,则AH=![]() x,AD=2x,∴AM=4+2x,∴BH=4+2x,
x,AD=2x,∴AM=4+2x,∴BH=4+2x,
∵四边形ABDE是平行四边形,∴DF∥AB,∴![]() ,
,
∴![]() ,解得x=
,解得x=![]() 或
或![]() (舍弃),
(舍弃),
∴DH=![]() .
.


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:初中数学 来源: 题型:
【题目】我市开展“美丽自宫,创卫同行”活动,某校倡议学生利用双休日在“花海”参加义务劳动,为了解同学们劳动情况,学校随机调查了部分同学的劳动时间,并用得到的数据绘制了不完整的统计图,根据图中信息回答下列问题:
(1)将条形统计图补充完整;
(2)扇形图中的“1.5小时”部分圆心角是多少度?
(3)求抽查的学生劳动时间的众数、中位数.

查看答案和解析>>
科目:初中数学 来源: 题型:
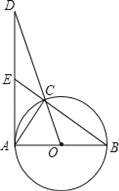
【题目】如图,已知AB是⊙O的直径,点C为圆上一点,点D在OC的延长线上,连接DA,
交BC的延长线于点E,使得∠DAC=∠B.
(1)求证:DA是⊙O切线;
(2)求证:△CED∽△ACD;
(3)若OA=1,sinD=![]() ,求AE的长.
,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场第一次用11000元购进某款拼装机器人进行销售,很快销售一空,商家又用24000元第二次购进同款机器人,所购进数量是第一次的2倍,但单价贵了10元.
(1)求该商家第一次购进机器人多少个?
(2)若所有机器人都按相同的标价销售,要求全部销售完毕的利润率不低于20%(不考虑其它因素),那么每个机器人的标价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市有两家出租车公司,收费标准不同,甲公司收费标准为:起步价8元,超过3千米后,超过的部分按照每千米1.5元收费.乙公司收费标准为:起步价11元,超过3千米后,超过的部分按照每千米1.2元收费.车辆行驶![]() 千米.本题中
千米.本题中![]() 取整数,不足
取整数,不足![]() 的路程按
的路程按![]() 计费.
计费.
根据上述内容,完成以下问题:
(1)当![]() ,乙公司比甲公司贵________元.
,乙公司比甲公司贵________元.
(2)当![]() ,且
,且![]() 为整数时,甲、乙两公司的收费分别是多少?(结果用化简后的含
为整数时,甲、乙两公司的收费分别是多少?(结果用化简后的含![]() 的式子表示)
的式子表示)
(3)当行驶路程为12千米时,哪家公司的费用更便宜?便宜多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店第一次用600元购进2B铅笔若干支,第二次又用600元购进该款铅笔,但这次每支的进价是第一次进价的![]() 倍,购进数量比第一次少了30支.
倍,购进数量比第一次少了30支.
(1)求第一次每支铅笔的进价是多少元?
(2)若要求这两次购进的铅笔按同一价格全部销售完毕后获利不低于420元,问每支售价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数轴上,点A、B分别表示有理数a、b,则 |a-b| 可以表示点A、B之间的距离,如|a-2| =1表示到点2的距离等于1的点,a=3或1.
按照要求在数轴上标出点A的位置,并写出a的值.
(1)若 |a-0| =3,则a=________;
![]()
(2)若 |a-1| =3,则a=_______;
![]()
(3)若 |a+1| =3,则a=__________;
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com