
【题目】已知:如图,在△ABC中,BC=AC,以BC为直径的⊙O与边AB相交于点D,DE⊥AC,垂足为点E.
(1)求证:点D是AB的中点;
(2)判断DE与⊙O的位置关系,并证明你的结论;
(3)若⊙O的直径为18,cosB= ![]() ,求DE的长.
,求DE的长.
【答案】
(1)证明:连接CD,
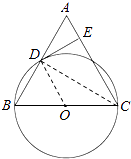
∵BC为⊙O的直径,∴CD⊥AB,
又∵AC=BC,
∴AD=BD,即点D是AB的中点
(2)解:DE是⊙O的切线.
证明:连接OD,则DO是△ABC的中位线,
∴DO∥AC,
又∵DE⊥AC,
∴DE⊥DO即DE是⊙O的切线
(3)解:∵AC=BC,∴∠B=∠A,
∴cosB=cosA= ![]() ,
,
∵cosB= ![]() ,BC=18,
,BC=18,
∴BD=6,
∴AD=6,
∵cosA= ![]() ,
,
∴AE=2,
在Rt△AED中,DE= ![]() .
.
【解析】(1)连接CD,利用圆周角定理得出CD⊥AB,又由等腰三角形的三线合一得出点D是AB的中点;(2)连接OD,则DO是△ABC的中位线,利用中位线定理得DO∥AC,又因DE⊥AC从而得出DE⊥DO,进而得出结论;(3)根据余弦的定义得出BD的长度,从而得出AD的长度,再根据等角的余弦相等得出AE的长度,最后用勾股定理得出答案。


科目:初中数学 来源: 题型:
【题目】若两个二次函数图象的顶点、开口方向都相同,则称这两个二次函数为“同簇二次函数”
(1)请直接写出两个为“同簇二次函数”的函数:①______,②_________;
(2)已知关于![]() 的二次函数
的二次函数![]() 和
和![]() ,若
,若![]() 与
与![]() 为“同簇二次函数”,求函数
为“同簇二次函数”,求函数![]() 的表达式,并求出当
的表达式,并求出当![]() 时,
时,![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD的对角线交于点O,且AB≠AD,过O作OE⊥BD交BD于点E.若△CDE的周长为10,则平行四边形ABCD的周长为( )
A.10
B.16
C.18
D.20
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为了建设国家级卫生城市.市政部门决定搭配A、B两种园艺造型共50个摆放在市区,现有3490盆甲种花卉和2950盆乙种花卉可供使用,已知搭配一个A种造型需甲种花卉80盆,乙种花卉40盆,搭配一个B种造型需甲种花卉50盆,乙种花卉90盆.
(1)问符合题意的搭配方案有几种?请你帮助设计出来.
(2)若搭配一个A种造型的费用是800元,搭配一个B种造型的费用是960元,试说明(1)中哪种方案费用最低?最低费用是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,广安市防洪指挥部发现渠江边一处长400米,高8米,背水坡的坡角为45°的防洪大堤(横截面为梯形ABCD)急需加固.经调查论证,防洪指挥部专家组制定的加固方案是:背水坡面用土石进行加固,并使上底加宽2米,加固后,背水坡EF的坡比i=1:2.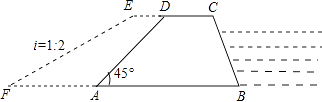
(1)求加固后坝底增加的宽度AF的长;
(2)求完成这项工程需要土石多少立方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自从新冠肺炎疫情爆发,我国高度重视并采取了强有力的措施进行防控,像钟南山爷爷和李兰娟奶奶等无数白衣天使为保卫大家的安全奋斗在抗疫一线. 武汉是疫情最先爆发的地区,“一方有难,八方支援”是中华传统美德,为了帮助武汉人民尽快度过难关,某校七年级全体同学参加了捐款活动.现随机抽查了部分同学捐款的情况统计如图所示:

(1)在本次调查中,一共抽查了_________名学生;
(2)请补全条形统计图,并计算在扇形统计图中,“捐款 20元”对应的圆心角度数是 度;
(3)在七年级600名学生中,捐款15元以上(不含15元)的学生估计有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:用3辆A型车和2辆B型车载满货物一次可运货17吨;用2辆A型车和3辆B型车载满货物一次可运货l8吨,某物流公刊现有35吨货物,计划同时租用A型车a辆,B型车b辆,一次运完,且恰好每辆车都载满货物.
根据以上信息,解答下列问题:
(1)l辆A型车和l辆B型车都载满货物一次可分别运货多少吨?
(2)请你帮该物流公司设计租车方案;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,![]() ,且满足式子
,且满足式子![]() .
.
(1)求出![]() 的值;
的值;
(2)①在![]() 轴的正半轴上存在一点
轴的正半轴上存在一点![]() ,使
,使![]() 的面积等于
的面积等于![]() 的面积的一半,求出点
的面积的一半,求出点![]() 的坐标;
的坐标;
②在坐标轴的其它位置是否存在点![]() ,使
,使![]() 的面积等于
的面积等于![]() 的面积的一半仍然成立,若存在,直接写出其他符合条件的点
的面积的一半仍然成立,若存在,直接写出其他符合条件的点![]() 的坐标;
的坐标;
(3)如图2,过点![]() 作
作![]() 轴交
轴交![]() 轴于点
轴于点![]() ,点
,点![]() 为线段
为线段![]() 延长线上一动点,连接
延长线上一动点,连接![]() ,
,![]() 平分
平分![]() ,
,![]() ,当点
,当点![]() 运动时,求证:
运动时,求证:![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD中,已知∠BAD=120°,∠EGF=60°, ∠EGF的顶点G在菱形对角线AC上运动,角的两边分别交边BC、CD于E、F.
[Failed to download image : http://192.168.0.10:8086/QBM/2018/5/2/1936696631435264/1937624997150720/STEM/6b570bc424f747a8be031e9f971720ec.png]
(1)如图甲,当顶点G运动到与点A重合时,求证:EC+CF=BC;
(2)知识探究:
①如图乙,当顶点G运动到AC的中点时,请直接写出线段EC、CF与BC的数量关系(不需要写出证明过程);
②如图丙,在顶点G运动的过程中,若![]() ,探究线段EC、CF与BC的数量关系;
,探究线段EC、CF与BC的数量关系;
(3)问题解决:如图丙,已知菱形的边长为8,BG=7,CF=![]() ,当
,当![]() >2时,求EC的长度。
>2时,求EC的长度。
[Failed to download image : http://192.168.0.10:8086/QBM/2018/5/2/1936696631435264/1937624997150720/STEM/1671b8ec524a49feac7097357d4ff9a8.png]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com