【题目】如图，在平面直角坐标系中，一次函数
的图像经过点
，且与
轴相交于点
，与正比例函数
的图像交于点
，点的横坐标为
．
（1）求
的值；
（2）若点
在
轴上，且满足
，求点的坐标．
【答案】（1）k=-1，b=4（2）（0，12）或（0，-12）
【解析】
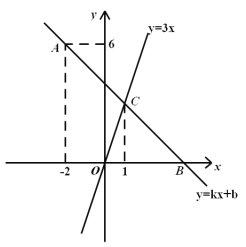
(1)由图形可知，点C的横坐标为1，利用一次函数图象上点的坐标特征可求出点C的坐标；根据点A、C的坐标，利用待定系数法即可求出k、b的值；
(2)先利用一次函数求出点B的坐标，设点D的坐标为(0，m)，结合
，得出关于m的一元一次方程；接下来解方程，即可得出m的值，进而可得点D的坐标.
解：(1)当x=1时，y=3x=3，
∴点C的坐标为(1，3).
将A(-2，6)，C(1，3)代入y=kx+b得
解得k=1，b=4；
(2)当y=0时，有-x+4=0，
解得：x=4，
∴点B的坐标为(4，0).
设点D的坐标为(0，m)(m＜0)，
∵S△COD=S△BOC，
∴
|m|=×4×3，
解得m=12，或m=-12
∴点D的坐标为(0，12)或(0，12).
故答案为：(1)k=-1，b=4；(2)(0，12)或(0，-12).
开心快乐假期作业暑假作业西安出版社系列答案
名题训练系列答案
期末集结号系列答案科目：初中数学 来源： 题型：
【题目】根据题意完成下列推理过程：
已知：如图，已知
，
，垂足分别为
、
，
．求证：
．
证明：
，（已知）
（垂直的定义）
（__________）
__________（__________）
又
（已知）
__________
（__________）
（__________）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知关于x的一元二次方程x2－4x－m2=0
（1）求证：该方程有两个不等的实根；
（2）若该方程的两实根x1、x2满足x1+2x2=9，求m的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知直线l1∥l2，直线l3和直线l1、l2交于点C和D，点P是直线l3上一动点
（1）如图1，当点P在线段CD上运动时，∠PAC，∠APB，∠PBD之间存在什么数量关系？请你猜想结论并说明理由．
（2）当点P在C、D两点的外侧运动时（P点
与点C、D不重合，如图2和图3），上述（1）中的结论是否还成立？若不成立，请直接写出∠PAC，∠APB，∠PBD之间的数量关系，不必写理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在矩形ABCD中，AB=4，AD=5，AD，AB，BC分别与⊙O相切于E，F，G三点，过点D作⊙O的切线BC于点M，切点为N，则DM的长为（ ）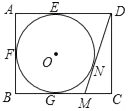
A.
B.
C.
D.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知直线a，b被直线c，d所截，直线a，c，d相交于点O，按要求完成下列各小题．
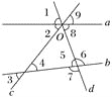
(1)在图中的∠1～∠9这9个角中，同位角共有多少对？请你全部写出来；
(2)∠4和∠5是什么位置关系的角？∠6和∠8之间的位置关系与∠4和∠5的相同吗？
查看答案和解析>>
科目：初中数学 来源： 题型：
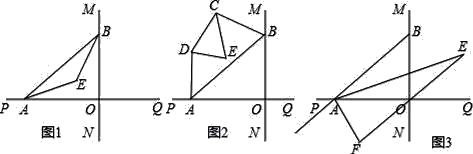
【题目】直线MN与直线PQ垂直相交于O，点A在直线PQ上运动，点B在直线MN上运动．
（1）如图1，已知AE、BE分别是∠BAO和∠ABO角的平分线，点A、B在运动的过程中，∠AEB的大小是否会发生变化？若发生变化，请说明变化的情况；若不发生变化，试求出∠AEB的大小．
（2）如图2，已知AB不平行CD，AD、BC分别是∠BAP和∠ABM的角平分线，又DE、CE分别是∠ADC和∠BCD的角平分线，点A、B在运动的过程中，∠CED的大小是否会发生变化？若发生变化，请说明理由；若不发生变化，试求出其值．
（3）如图3，延长BA至G，已知∠BAO、∠OAG的角平分线与∠BOQ的角平分线及延长线相交于E、F，在△AEF中，如果有一个角是另一个角的3倍，试求∠ABO的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】对于三个数
，用
表示这三个数中最大数，例如：
，
解决问题：
（1）填空：
{
，
，
}= ，如果{，
，
}=，则
的取值范围为 ；
（2）如果{，
，
}=
，求的值；
（3）如图，在同一坐标系中画出了三个一次函数的图象：
，
和
请观察这三个函数的图象，
①在图中画出{
，
，
}对应的图像（加粗）；
②{，
，}的最小值为 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
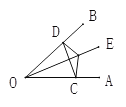
【题目】如图，点E是∠AOB的平分线上一点，EC⊥OA，ED⊥OB，垂足分别为C、D．
求证：（1）∠ECD=∠EDC；
（2）OC=OD；
（3）OE是线段CD的垂直平分线．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com