
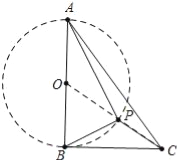
【题目】如图,Rt△ABC中,AB⊥BC,AB=6,BC=4,P是△ABC内部的一个动点,且满足∠PAB=∠PBC,则线段CP长的最小值为( ).

A. 4 B. ![]() C.
C. ![]() D. 2
D. 2
【答案】D
【解析】首先证明点P在以AB为直径的⊙O上,连接OC与⊙O交于点P,此时PC最小,利用勾股定理求出OC即可解决问题.
解:∵∠ABC=90°,
∴∠ABP+∠PBC=90°,
∵∠PAB=∠PBC,
∴∠BAP+∠ABP=90°,
∴∠APB=90°,
∴点P在以AB为直径的⊙O上,连接OC交⊙O于点P,此时PC最小,
在RT△BCO中,∵∠OBC=90°,BC=4,OB=3,
∴OC=![]() =5,
=5,
∴PC=OC=OP=5﹣3=2.
∴PC最小值为2.
故选B.
“点睛”本题考查了点与圆位置关系、圆周角定理、最短问题等知识,解题关键是确定点P位置,学会求圆外一点到圆的最小、最大距离,属于中考常考题型.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,过A(-2, 0), C(0, 6)两点的抛物线y=-![]() x2+ax+b与x轴交于另一点B,点D是抛物线的顶点.
x2+ax+b与x轴交于另一点B,点D是抛物线的顶点.
(1)求a、b的值;
(2)点P是x轴上的一个动点,过P作直线l//AC交抛物线于点Q.随着点P的运动,若以A、P、Q、C为顶点的四边形是平行四边形,请直接写出符合条件的点Q的坐标;
(3)在直线AC上是否存在一点M,使△BDM的周长最小,若存在,请找出点M并求出点M的坐标.若不存在,请说明理由。


备用图
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,△ABC是边长3cm的等边三角形.动点P以1cm/s的速度从点A出发,沿线段AB向点B运动.
(1)如图1,设点P的运动时间为t(s),那么t为何值时,△PBC是直角三角形;
(2)若另一动点Q从点C出发,沿射线BC方向运动.连接PQ交AC于D.如果动点P,Q都以1cm/s的速度同时出发.
①如图2,设运动时间为t(s),那么t为何值时,△DCQ是等腰三角形?
②如图3,连接PC,请你猜想:在点P,Q的运动过程中,△PCD和△QCD的面积有什么关系?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,E,F,G,H依次是各边中点,O是四边形内一点,若S四边形AEOH=3,S四边形BFOE=4,S四边形CGOF=5,则S四边形DHOG= . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是△ABC边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
(Ⅰ)求证:OE=OF;
(Ⅱ)若CE=8,CF=6,求OC的长;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD的外侧,作两个等边三角形ADE和DCF,连接AF,BE.
(Ⅰ)请写出AF与BE的数量关系与位置关系分别是什么,并证明.
(Ⅱ)如图2,若将条件“两个等边三角形ADE和DCF”变为两个等腰三角形ADE和DCF,且EA=ED=FD=FC,第(1)问中的结论是否仍然成立?请作出判断并给予证明;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某药品包装盒上标注着“贮藏温度:1℃土2℃”,以下是几个保存柜的温度,适合贮藏药品的温度是( )
A. -4℃ B. 0℃ C. 4℃ D. 5℃
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com