
分析 (1)根据题意得到抛物线为y=(x-2)2-3,整理成一般式即可求得b,c的值;
(2)令y=1,判断所得方程的判别式大于0即可求解;
(3)求得函数的对称轴是x=b,然后分成b≤-2,-2<b<2和b≥2三种情况进行讨论,然后根据最小值是-3,即可解方程求解.
解答 解:(1)∵抛物线y=x2-2bx+c
∴a=1,
∵抛物线的顶点坐标为(2,-3),
∴y=(x-2)2-3,
∵y=(x-2)2-3=x2-4x+1,
∴b=2,c=1;
(2)由y=1得 x2-2bx+c=1,
∴x2-2bx+c-1=0
∵△=4b2+4b+4=(2b+1)2+3>0,
则存在两个实数,使得相应的y=1;
(3)由c=b+2,则抛物线可化为y=x2-2bx+b+2,其对称轴为x=b,
①当x=b≤-2时,则有抛物线在x=-2时取最小值为-3,此时
-3=(-2)2-2×(-2)b+b+2,解得b=-$\frac{9}{5}$,不合题意;
②当x=b≥2时,则有抛物线在x=2时取最小值为-3,此时
-3=22-2×2b+b+2,解得b=3,
③当-2<b<2时,则$\frac{4(b+2)-4{b}^{2}}{4}$=-3,化简得:b2-b-5=0,解得:
b1=$\frac{1+\sqrt{21}}{2}$(不合题意,舍去),b2=$\frac{1-\sqrt{21}}{2}$.
综上:b=3或$\frac{1-\sqrt{21}}{2}$.
点评 本题考查了二次函数的性质以及函数的最值,注意讨论对称轴的位置是本题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
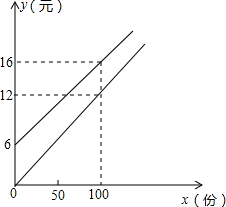 某校实行学案式教学,需印制若干份数学学案,印刷厂有甲、乙两种收费方式,除按印数收取印刷费外,甲种方式还需收取制版费而乙钟不需要,两种印刷方式的收费用y(元)与印刷份数x(份)之间的函数关系如图所示:
某校实行学案式教学,需印制若干份数学学案,印刷厂有甲、乙两种收费方式,除按印数收取印刷费外,甲种方式还需收取制版费而乙钟不需要,两种印刷方式的收费用y(元)与印刷份数x(份)之间的函数关系如图所示:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
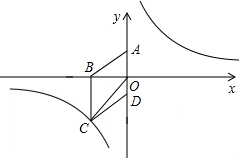 如图,在平面直角坐标系中,已知四边形ABCD是菱形.且A,B两点的坐标分别为(0,3),(-4,0).
如图,在平面直角坐标系中,已知四边形ABCD是菱形.且A,B两点的坐标分别为(0,3),(-4,0).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
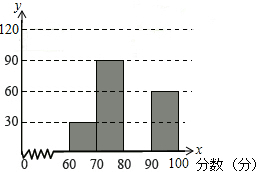 某校举行了一场学生“安全知识”问答竞赛活动,为了解笔试情况,随机抽查了部分学生的得分情况,请根据图表提供的信息,解答下列问题:
某校举行了一场学生“安全知识”问答竞赛活动,为了解笔试情况,随机抽查了部分学生的得分情况,请根据图表提供的信息,解答下列问题:| 分数段 | 频数 | 频率 |
| 60≤x<70 | 30 | 0.1 |
| 70≤x<80 | 90 | n |
| 80≤x<90 | m | 0.4 |
| 90≤x<100 | 60 | 0.2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com