练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】将一张矩形纸片ABCD如图所示那样折起，使顶点C落在C′处，其中AB=4，若∠C′ED=30°，则折痕ED的长为（ ）
    A.4
    B.
    C.8
    D.

    【答案】C
    【解析】解：由翻折变换得到，C′D=DC=AB=4，∠C′=90°，又因为∠C′ED=30°，所以ED=8． 故选C．
    【考点精析】根据题目的已知条件，利用翻折变换（折叠问题）和解直角三角形的相关知识可以得到问题的答案，需要掌握折叠是一种对称变换，它属于轴对称，对称轴是对应点的连线的垂直平分线，折叠前后图形的形状和大小不变，位置变化，对应边和角相等；解直角三角形的依据：①边的关系a2+b2=c2；②角的关系：A+B=90°；③边角关系：三角函数的定义．(注意：尽量避免使用中间数据和除法)．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知抛物线y=ax2+bx+c（a≠0）上部分点的横坐标x与纵坐标y的对应值如下表：

    x

    …

    ﹣1

    0

    2

    3

    4

    …

    y

    …

    5

    2

    2

    5

    10

    …


    （1）根据上表填空： ①这个抛物线的对称轴是 ， 抛物线一定会经过点（﹣2，）；
    ②抛物线在对称轴右侧部分是（填“上升”或“下降”）；
    （2）如果将这个抛物线y=ax2+bx+c向上平移使它经过点（0，5），求平移后的抛物线表达式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，PA、PB是⊙O的切线，A、B是切点，点C是劣弧AB上的一个动点，若∠ACB=110°，则∠P的度数是（ ）
    A.55°
    B.30°
    C.35°
    D.40°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】若二次函数y=x2+mx的对称轴是x=3，则关于x的方程x2+mx=7的解为（　　）
    A.x1=0，x2=6
    B.x1=1，x2=7
    C.x1=1，x2=﹣7
    D.x1=﹣1，x2=7

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】秋季新学期开学时，红城中学对七年级新生掌握“中学生日常行为规范”的情况进行了知识测试，测试成绩全部合格，现学校随机选取了部分学生的成绩，整理并制作成了如下不完整的图表：

    分　数　段

    频数

    频率

    60≤x＜70

    9

    a

    70≤x＜80

    36

    0.4

    80≤x＜90

    27

    b

    90≤x≤100

    c

    0.2


    请根据上述统计图表，解答下列问题：
    （1）在表中，a= ， b= ， c=；
    （2）补全频数直方图；
    （3）根据以上选取的数据，计算七年级学生的平均成绩．
    （4）如果测试成绩不低于80分者为“优秀”等次，请你估计全校七年级的800名学生中，“优秀”等次的学生约有多少人？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，点O为原点，菱形OABC的对角线OB在x轴上，顶点A在反比例函数y= 的图像上，则菱形的面积为 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知△ABC，△DCE，△FEG是三个全等的等腰三角形，底边BC，CE，EG在同一直线上，且AB= ，BC=1，连结BF，分别交AC，DC，DE于点P，Q，R．

    （1）求证：△BFG∽△FEG，并求出BF的长；
    （2）求AP：PC的值；
    （3）观察图形，请你提出一个与点P相关的问题，并进行解答．（根据提出问题的层次和解答过程平分）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，∠C=90°，在AB边上取一点D，使BD=BC，过D作DE⊥AB交AC于E，AC=8，BC=6．求DE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知反比例函数y1= 与一次函数y2=k2x+b的图象交于点A（1，8），B（﹣4，m）两点．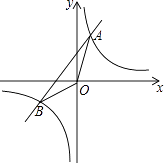
    （1）求k1 ， k2 ， b的值；
    （2）求△AOB的面积；
    （3）请直接写出不等式 x+b的解．

    查看答案和解析>>

    同步练习册答案