
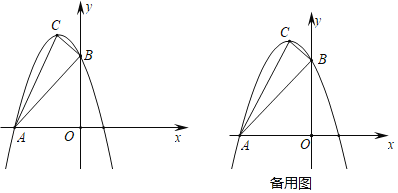
【题目】如图已知抛物线y=﹣x2+(1﹣m)x﹣m2+12交x轴于点A,交y轴于点B(0,3),顶点C位于第二象限,连接AB,AC,BC.
(1)求抛物线的解析式;
(2)在x轴上是否存在点P,使得△PAB的面积等于△ABC的面积?如果存在,求出点P的坐标.
(3)将△ABC沿x轴向右移动t个单位长度(0<t<1)时,平移后△ABC和△ABO重叠部分的面积为S,求S与t之间的函数关系.
【答案】(1)y=﹣x2﹣2x+3;(2)点P的坐标为(﹣1,0)或(﹣5,0);(3)![]()
【解析】
(1)利用二次函数图象上点的坐标特征可求出m的值,结合抛物线的顶点在第二象限可得出m>1,进而可确定m的值,再将其代入抛物线解析式中即可得出结论;
(2)过点C作CD⊥x轴,垂足为点D,利用二次函数图象上点的坐标特征及配方法,可求出点A,C的坐标,利用分割图形求面积法可求出△ABC的面积,再由三角形的面积公式结合S△PAB=S△ABC可求出AP的长,结合点A的坐标,即可求出点P的坐标;
(3)设△ABC平移后得到△A′B′C′,A′B′与y轴交于点M,A′C′交AB于点N,根据点的坐标,利用待定系数法可求出线段AB,AC所在直线的解析式,结合平移的性质可得出线段A′B′,A′C′所在直线的解析式,利用一次函数图象上点的坐标特征可求出点M,N的坐标,由三角形、梯形的面积公式结合S=S△AOB﹣S△AA′N﹣S△AA′M,即可得出S关于t的函数关系式.
(1)∵抛物线y=﹣x2+(1﹣m)x﹣m2+12交y轴于点B(0,3),
∴﹣m2+12=3,
∴m=±3.
又∵抛物线的顶点C位于第二象限,
∴﹣![]() ,
,
∴m>1,
∴m=3,
∴抛物线的解析式为y=﹣x2﹣2x+3.
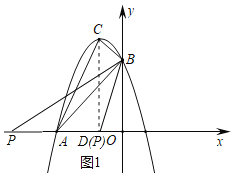
(2)过点C作CD⊥x轴,垂足为点D,如图1所示.
当y=0时,﹣x2﹣2x+3=0,
解得:x1=﹣3,x2=1,
∴点A的坐标为(﹣3,0).
∵y=﹣x2﹣2x+3=﹣(x+1)2+4,
∴点C的坐标为(﹣1,4),点D的坐标为(﹣1,0),
∴S△ABC=S△ACD+S梯形CDOB﹣S△AOB,
=![]() ADCD+
ADCD+![]() (OB+CD)OD﹣
(OB+CD)OD﹣![]() OAOB,
OAOB,
=![]() ×2×4+
×2×4+![]() ×(3+4)×1﹣
×(3+4)×1﹣![]() ×3×3,
×3×3,
=3.
∵S△PAB=S△ABC,
∴![]() APOB=3,
APOB=3,
∴AP=2,
∴点P的坐标为(﹣1,0)或(﹣5,0).
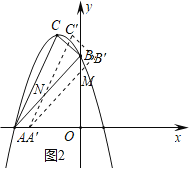
(3)设△ABC平移后得到△A′BC′,A′B′与y轴交于点M,A′C′交AB于点N,如图2所示.
设线段AB所在直线的解析式为y=kx+b(k≠0),
将A(﹣3,0),B(0,3)代入y=kx+b,得:
![]() ,解得:
,解得:![]() ,
,
∴线段AB所在直线的解析式为y=x+3.
同理,可得出线段AC所在直线的解析式为y=2x+6.
∵将△ABC沿x轴向右移动t个单位长度(0<t<1)得到△A′B′C′,
∴点A′的坐标为(t﹣3,0),线段A′B′所在直线的解析式为y=x+3﹣t(0<t<1),线段A′C′所在直线的解析式为y=2x+6﹣2t(0<t<1).
当x=0时,y=x+3﹣t=3﹣t,
∴点M的坐标为(0,3﹣t).
将y=x+3代入y=2x+6﹣2t,整理,得:x+3﹣2t=0,
解得:x=2t﹣3,
∴点N的坐标为(2t﹣3,2t),
∴S=S△AOB﹣S△AA′N﹣S△AA′M,
=![]() OAOB﹣
OAOB﹣![]() AA′yA′﹣
AA′yA′﹣![]() OA′OM,
OA′OM,
=![]() ×3×3﹣
×3×3﹣![]() t2t﹣
t2t﹣![]() (3﹣t)(3﹣t),
(3﹣t)(3﹣t),
=﹣![]() t2+3t.
t2+3t.
∴S与t之间的函数关系式为S=﹣![]() t2+3t(0<t<1).
t2+3t(0<t<1).


科目:初中数学 来源: 题型:
【题目】我市倡导垃圾分类投放,将日常垃圾分成四类,分别投放四种不同颜色的垃圾桶中,在“垃圾分类”模拟活动中,某同学把两个不同类的垃圾随意放入两个不同颜色的垃圾筒中,则这个同学正确分类投放垃圾的概率是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
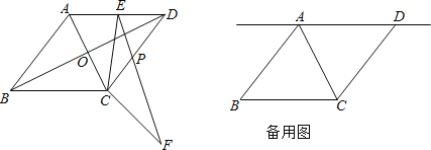
【题目】如图,在菱形ABCD中,对角线AC、BD交于点O,已知AC=2![]() ,AB=5.
,AB=5.
(1)求BD的长;
(2)点E为直线AD上的一个动点,连接CE,将线段EC绕点C顺时针旋转∠BCD的角度后得到对应的线段CF(即∠ECF=∠BCD),EF交CD于点P.
①当E为AD的中点时,求EF的长;
②连接AF、DF,当DF的长度最小时,求△ACF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
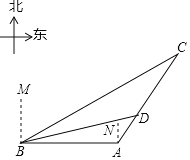
【题目】今年,我国海关总署严厉打击“洋垃圾”违法行动,坚决把“洋垃圾”拒于国门之外.如图,某天我国一艘海监船巡航到A港口正西方的B处时,发现在B的北偏东60°方向,相距150海里处的C点有一可疑船只正沿CA方向行驶,C点在A港口的北偏东30°方向上,海监船向A港口发出指令,执法船立即从A港口沿AC方向驶出,在D处成功拦截可疑船只,此时D点与B点的距离为75![]() 海里.
海里.
(1)求B点到直线CA的距离;
(2)执法船从A到D航行了多少海里?(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A在双曲线y=的第一象限的那一支上,AB垂直于x轴与点B,
点C在x轴正半轴上,且OC=2AB,点E在线段AC上,且AE=3EC,点D为OB的中点,若△ADE
的面积为3,则k的值为 ▲ .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种文具,进价为5元/件.售价为6元/件时,当天的销售量为100件.在销售过程中发现:售价每上涨0.5元,当天的销售量就减少5件.设当天销售单价统一为![]() 元/件(
元/件(![]() ,且
,且![]() 是按0.5元的倍数上涨),当天销售利润为
是按0.5元的倍数上涨),当天销售利润为![]() 元.
元.
(1)求![]() 与
与![]() 的函数关系式(不要求写出自变量的取值范围);
的函数关系式(不要求写出自变量的取值范围);
(2)要使当天销售利润不低于240元,求当天销售单价所在的范围;
(3)若每件文具的利润不超过![]() ,要想当天获得利润最大,每件文具售价为多少元?并求出最大利润.
,要想当天获得利润最大,每件文具售价为多少元?并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
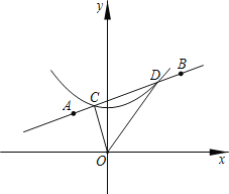
【题目】如图,在平面直接坐标系中,将反比例函数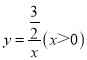 的图象绕坐标原点O逆时针旋转45°得到的曲线l,过点
的图象绕坐标原点O逆时针旋转45°得到的曲线l,过点![]() ,
,![]()
![]() 的直线与曲线l相交于点C、D,则sin∠COD=___ .
的直线与曲线l相交于点C、D,则sin∠COD=___ .
查看答案和解析>>
科目:初中数学 来源: 题型:
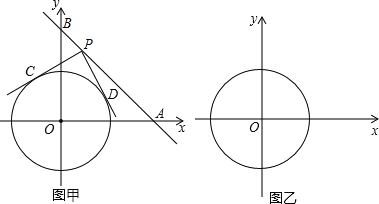
【题目】如图甲,在平面直角坐标系中,直线分别交x轴、y轴于点A、B,⊙O的半径为![]() 个单位长度,点P为直线y=﹣x+6上的动点,过点P作⊙O的切线PC、PD,切点分别为C、D,且PC⊥PD.
个单位长度,点P为直线y=﹣x+6上的动点,过点P作⊙O的切线PC、PD,切点分别为C、D,且PC⊥PD.
(1)判断四边形OCPD的形状并说明理由.
(2)求点P的坐标.
(3)若直线y=﹣x+6沿x轴向左平移得到一条新的直线y1=﹣x+b,此直线将⊙O的圆周分得两段弧长之比为1:3,请直接写出b的值.
(4)若将⊙O沿x轴向右平移(圆心O始终保持在x轴上),试写出当⊙O与直线y=﹣x+6有交点时圆心O的横坐标m的取值范围.(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电视台的一档娱乐性节目中,在游戏PK环节,为了随机分选游戏双方的组员,主持人设计了以下游戏:用不透明的白布包住三根颜色长短相同的细绳AA1、BB1、CC1,只露出它们的头和尾(如图所示),由甲、乙两位嘉宾分别从白布两端各选一根细绳,并拉出,若两人选中同一根细绳,则两人同队,否则互为反方队员.
(1)若甲嘉宾从中任意选择一根细绳拉出,求他恰好抽出细绳AA1的概率;
(2)请用画树状图法或列表法,求甲、乙两位嘉宾能分为同队的概率.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com