
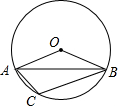
 如图,在⊙O中,已知∠OAB=22.5°,则∠C的度数为( )
如图,在⊙O中,已知∠OAB=22.5°,则∠C的度数为( )| A. | 122.5° | B. | 135° | C. | 112.5° | D. | 115.5° |
分析 作AB弧所对的圆周角∠APB,如图,利用等腰三角形的性质和三角形内角和得∠AOB=135°,则根据圆周角定理得到∠P=$\frac{1}{2}$∠AOB=67.5°,然后根据圆周角定理可计算出∠ACB的度数.
解答 解:作AB弧所对的圆周角∠APB,如图,
∵OA=OB,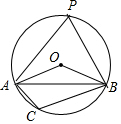
∴∠OBA=∠OAB=22.5°,
∴∠AOB=180°-2×22.5°=135°,
∴∠P=$\frac{1}{2}$∠AOB=67.5°,
∴∠ACB=180°-67.5°=112.5°.
故选C.
点评 本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
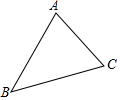 (1)用直尺和圆规作出如图三角形ABC的外接圆⊙O (不写作法,保留作图痕迹).
(1)用直尺和圆规作出如图三角形ABC的外接圆⊙O (不写作法,保留作图痕迹).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com