
【题目】抛物线![]() 与y轴交于点
与y轴交于点![]() .
.
(1)求抛物线的解析式;
(2)求抛物线与坐标轴的交点坐标;
(3)①当x取什么值时, ![]() ?
? ![]() 当x取什么值时,y的值随x的增大而减小?
当x取什么值时,y的值随x的增大而减小?
【答案】(1)![]() ;(2)x轴:
;(2)x轴: ![]() 、
、![]() ;Y轴:
;Y轴: ![]()
(3)见解析.
【解析】试题分析:(1)将点(0,3)代入抛物线的解析式中,即可求得m的值;
(2)可以令y=0,可得出一个关于x的一元二次方程,方程的解就是抛物线与x轴交点的横坐标;
(3)根据(2)中抛物线与x轴的交点以及抛物线的开口方向即可求得x的取值范围.
试题解析:(1)将点(0,3)代入抛物线y=-x2+(m-1)x+m,
m=3,
∴抛物线的解析式y=-x2+2x+3;
(2)令y=0,-x2+2x+3=0,
解得x1=3,x2=-1;
x轴:A(3,0)、B(-1,0);
y轴:C(0,3)
(3)抛物线开口向下,对称轴x=1;
所以)①当-1<x<3时,y>0;
②当x≥1时,y的值随x的增大而减小.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案科目:初中数学 来源: 题型:
【题目】如图是二次函数![]() 图象的一部分,其对称轴是
图象的一部分,其对称轴是![]() ,且过点
,且过点![]() ,下列说法:①
,下列说法:①![]() ;②
;②![]() ;③
;③![]() ;④若
;④若![]() 是抛物线上两点,则
是抛物线上两点,则![]() ,其中说法正确的是( )
,其中说法正确的是( )

A. ①② B. ②③
C. ①②④ D. ②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(方法回顾)
(1)如图1,过正方形ABCD的顶点A作一条直l交边BC于点P,BE⊥AP于点E,DF⊥AP于点F,若DF=2.5,BE=1,则EF= .

(问题解决)
(2)如图2,菱形ABCD的边长为1.5,过点A作一条直线l交边BC于点P,且∠DAP=90°,点F是AP上一点,且∠BAD+∠AFD=180°,过点B作BE⊥AB,与直线l交于点E,若EF=1,求BE的长.
(思维拓展)
(3)如图3,在正方形ABCD中,点P在AD所在直线上的上方,AP=2,连接PB,PD,若△PAD的面积与△PAB的面积之差为m(m>0),则PB2﹣PD2的值为 .(用含m的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴上从左到右的三个点![]() ,
,![]() ,
,![]() 所对应的数分别为
所对应的数分别为![]() ,
,![]() ,
,![]() .其中
.其中![]() ,
,![]() ,如图所示.
,如图所示.
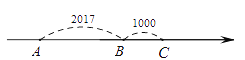
(1)若以![]() 为原点,写出点
为原点,写出点![]() ,
,![]() 所对应的数,并计算
所对应的数,并计算![]() 的值.
的值.
(2)若原点![]() 在
在![]() ,
,![]() 两点之间,求
两点之间,求![]() 的值.
的值.
(3)若![]() 是原点,且
是原点,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC为等边三角形,D、F分别为BC、AB上的点,且CD=BF,以AD为边作等边△ADE.
(1)求证:△ACD≌△CBF;
(2)点D在线段BC上何处时,四边形CDEF是平行四边形且![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】生活与数学
(1)吉姆同学在某月的日历上圈出2×2个数,正方形的方框内的四个数的和是32,那么第一个数是 ;

(2)玛丽也在上面的日历上圈出2×2个数,斜框内的四个数的和是42,则它们分别是 ;
![]()
(3)莉莉也在日历上圈出5个数,呈十字框形,它们的和是50,则中间的数是 ;

(4)某月有5个星期日的和是75,则这个月中最后一个星期日是 号;
(5)若干个偶数按每行8个数排成下图:
①图中方框内的9个数的和与中间的数的关系是 ;

②汤姆所画的斜框内9个数的和为360,则斜框的中间一个数是 ;

③托马斯也画了一个斜框,斜框内9个数的和为252,则斜框的中间一个数是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,BD=DF.
(1)求证:CF=EB.
(2)若AF=2,EB=1,求AB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上A点表示数a,B点表示数b,且a、b满足|a+2|+(b6)2=0![]()
(1)点A表示的数为 ;点B表示的数为 ;
(2)若点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC,请在数轴上找一点C,使AC=3BC,则C点表示的数 ;
(3)若在原点O处放一挡板,一小球甲从点A处以1个单位/秒的速度向左运动;同时另一小球乙从点B处以2个单位/秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看作一点)以原来的速度向相反的方向运动,设运动的时间为t(秒),请分别表示出甲、乙两小球到原点的距离(用t表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①、②、③、○n、…、M、N分别是⊙O的内接正三角形ABC、正方形ABCD、正五边形ABCDE、…、正n边形ABCDE…的边AB、BC上的点,且BM=CN,连接OM、ON.

(1)求图①中∠MON的度数;
(2)图②中∠MON的度数是_________,图③中∠MON的度数是___________;
(3)试探究∠MON的度数与正n边形边数n的关系(直接写出答案).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com