
����Ŀ����һ����ֱ�Ĺ�·����A��B���أ��������г���A�ص�B�أ��������г���B�ص�A�ڣ�����A�غ�������ԭ·���أ���ͼ�Ǽס���������B�صľ���y��km������ʻʱ��x��h��֮��ĺ���ͼ����ͼ�����������⣺
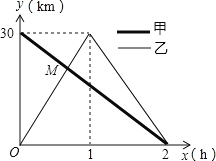
��1��A��B����֮��ľ��룺 km��
��2�����ٶ�Ϊ km/h���ҵ��ٶ�Ϊ30km/h��
��3����M������Ϊ ��
��4������B�صľ���y��km������ʻʱ��x��h��֮��ĺ�����ϵʽ������д���Ա�����ȡֵ��Χ����
���𰸡���1��30����2��15����3����![]() ��20������4��y=-15x+30��
��20������4��y=-15x+30��
��������
�����������1�����ݺ���ͼ��Ϳ��Եó�A��B���صľ��룻
��2�����ݺ���ͼ��Ӧ��ʱ�伴��������ҵ��ٶȣ�
��3�����ݺ���ͼ��Ӧ��ʱ�����������ҵ��ٶȣ��Ϳ����������ʱ�䣬�Ϳ����������B�صľ�����ó�������M�����ꣻ
��4�������B�صľ���y��km������ʻʱ��x��h���ĺ�����ϵʽΪy=kx+b���ѣ�0��20������2��0�����뼴�ɽ��
�����������1���ɺ���ͼ��
A��B���صľ���Ϊ30ǧ�ף�
��A��B���صľ���Ϊ30ǧ�ף�
��2���ɺ���ͼ��
���ٶ�Ϊ��30��2=15ǧ��/ʱ��
�ҵ��ٶ�Ϊ��30��1=30ǧ��/ʱ��
��3������������ʱ��Ϊ��30�£�15+30��=![]() Сʱ��
Сʱ��
����ʱ���뿪B�صľ���Ϊ��![]() ��30=20ǧ�ף�
��30=20ǧ�ף�
��M��![]() ��20����
��20����
��ʾ![]() Сʱʱ������������ʱ����B��20ǧ�ף�
Сʱʱ������������ʱ����B��20ǧ�ף�
��4���裺y=kx+b��
���������![]()
���k=-15��
������������ϵʽΪy=-15x+30��


 ��ʦ����ɳ���ʱͬ��ѧ����ϵ�д�
��ʦ����ɳ���ʱͬ��ѧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
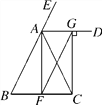
����Ŀ����ͼ��ƽ���ı���ABCD�У�BD��AD����A=45�㣬E��F�ֱ���AB��CD�ϵĵ㣬��BE=DF������EF��BD��O��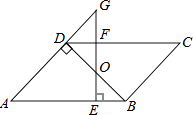
��1����֤��BO=DO��
��2����EF��AB���ӳ�EF��AD���ӳ�����G����FG=1ʱ����AE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�DZ߳�Ϊ4�������Σ��������ε�һ�����ϼ�ȥ������CEFG������E��G�ֱ��DZ�CD��BC�ϵĵ㣬��CE��3��CG��2��ʣ�ಿ����������ABGFED�����㽨���ʵ���ֱ������ϵ��������ABGFED����������꣮
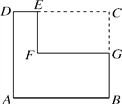
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����O�İ뾶OD����AB�ڵ�C������AO���ӳ�����O�ڵ�E������EC����AB=8��CD=2����EC�ij�Ϊ�� �� 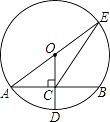
A.2 ![]()
B.8
C.2 ![]()
D.2 ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�ĶԽ���AC��BD�ཻ�ڵ�O��AC=6��BD=8������P�ӵ�B����������B��A��D������ABCD�ı����˶����˶�����Dֹͣ����P���ǵ�P����BD�ĶԳƵ㣬PP�佻BD�ڵ�M����BM=x����OPP������Ϊy����y��x֮��ĺ���ͼ�����Ϊ�� ��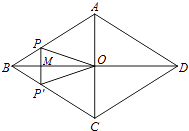
A.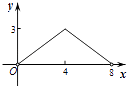
B.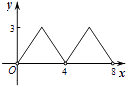
C.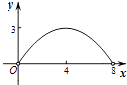
D.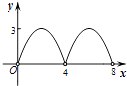
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����CAE�ǡ�ABC����ǣ�ADƽ�֡�EAC����AD��BC.����C��CG��AD������ΪG��AF��BC���ϵ����ߣ�����FG.
(1)��֤��AC��FG��
(2)��AC��FGʱ����ABCӦ�������������Σ�Ϊʲô��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������������̣�
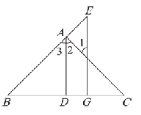
��ͼ��AD��BC�ڵ�D��EG��BC�ڵ�G��ADƽ�֡�BA C. ��֤�� ��E=��1.
֤���� ��AD��BC�ڵ�D��EG��BC�ڵ�G��(��֪)
���ADC=��EGC=90�㣬(��ֱ�Ķ���)
��AD��EG��( ������)
���1= ����������( ����������)
��E=��3��(��ֱ��ƽ�У�ͬλ�����)
��ADƽ�֡�BAC��(��֪)
���2=��3��( ��������)
���E=��1.(��������)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У�AB=4 cm��AD=12 cm����P��AD������ÿ��1 cm���ٶȴӵ�A���D�˶�����Q��BC���ϣ���ÿ��4 cm���ٶȴӵ�C��������CB�������˶���������ͬʱ����������P�����Dʱֹͣ(ͬʱ��QҲֹͣ)�������ʱ���ڣ����˶�ʱ��=_____ʱ�߶�PQ��AB.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ����Ʒ�ı��۸���200Ԫ�������ż��ڵı仯����Ʒ�ļ۸�ɸ���![]() ����һ�룮
����һ�룮
![]() �ĺ�����ʲô��
�ĺ�����ʲô��
![]() ������������Ʒ����۸����ͼ۸�
������������Ʒ����۸����ͼ۸�
![]() ����Ա���Ϊ�����������ۼǡ�
����Ա���Ϊ�����������ۼǡ�![]() �������ڱ��ۼǡ�
�������ڱ��ۼǡ�![]() ��������Ʒ�۸�ĸ�����Χ�ֿ���������ʾ��
��������Ʒ�۸�ĸ�����Χ�ֿ���������ʾ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com