
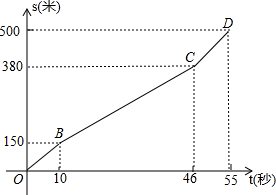
 为迎接2015短道速滑世界杯,中国短道速滑队进行多种强度的训练.在一次500m训练中,周洋所滑的路程s米与所用时间t秒之间的函数图象为折线OBCD.和她同时起滑的李坚柔前300m的速度保持在10m/s,后来速度改慢,但还保持匀速滑行,结果和周洋同时到达终点.
为迎接2015短道速滑世界杯,中国短道速滑队进行多种强度的训练.在一次500m训练中,周洋所滑的路程s米与所用时间t秒之间的函数图象为折线OBCD.和她同时起滑的李坚柔前300m的速度保持在10m/s,后来速度改慢,但还保持匀速滑行,结果和周洋同时到达终点.分析 (1)求出李坚柔前300米的时间就可以确定李坚柔300米时的图象位置E,再连接OE、DE就可以画出图象;
(2)根据函数图象求出周洋跑OB,BC,CD三段路程的速度,再比较大小就可以求出周洋的最快速度;
(3)运用待定系数法求出BC的解析式和OE的解析式,再根据一次函数与二元一次方程的关系就可以求出李坚柔在起跑后追上周洋同学的时间和离终点的距离.
解答 解:(1)由题意,得300÷10=30,
∴李坚柔运动中的图象经过E(30,300),
∴在平面直角坐标系中描出这点E,再连接OE,DE就可以画出李坚柔所跑的路程s(米)与所用时间t(秒)之间的函数图象,如图: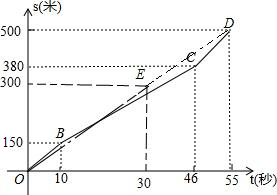
(2)由图象,得
周洋OB段的速度为:50÷10=5米/秒;
周洋BC段的速度为:(380-50)÷(46-10)=$\frac{55}{6}$米/秒;
周洋CD段的速度为:(500-380)÷(55-46)=$\frac{40}{3}$米/秒;
∴$\frac{40}{3}>\frac{55}{6}>5$,
∴周洋测试中的最快速度为$\frac{40}{3}$米/秒;
(3)设直线BC的解析式为y1=k1x+b1,设直线OE的解析式为y2=k2x,由题意,得
$\left\{\begin{array}{l}{10{k}_{1}+{b}_{1}=50}\\{46{k}_{1}+{b}_{1}=380}\\{300=30{k}_{2}}\end{array}\right.$
解得:$\left\{\begin{array}{l}{{k}_{1}=\frac{55}{6}}\\{{k}_{2}=10}\\{{b}_{1}=\frac{125}{3}}\end{array}\right.$,
则函数解析式是:y1=$\frac{55}{6}$x+$\frac{125}{3}$,y2=10x,
当y1=y2时,
$\frac{55}{6}$x+$\frac{125}{3}$=10x,
∴x=50,
当x=50时,
y2=50×10=500,
800-$\frac{2400}{7}$=$\frac{3200}{7}$.
答:李坚柔在起跑后 $\frac{480}{7}$秒追上周洋,这时她们距离终点还有 $\frac{3200}{7}$米.
点评 本题考查的是用一次函数解决实际问题,此类题是近年中考中的热点问题.注意一次函数图形的作法,在此题中作图关键是联系实际的变化,确定拐点.


 口算能手系列答案
口算能手系列答案科目:初中数学 来源: 题型:选择题
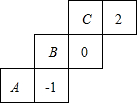 如图,是一个正方体纸盒的展开图,若在其中的三个正方形A,B,C内分别填入适当的数使得它们折成的正方体相对面上的两个数互为相反数,则填入正方形A,B,C内的三个数依次是( )
如图,是一个正方体纸盒的展开图,若在其中的三个正方形A,B,C内分别填入适当的数使得它们折成的正方体相对面上的两个数互为相反数,则填入正方形A,B,C内的三个数依次是( )| A. | 1,-2,0 | B. | 0,-2,1 | C. | -2,0,1 | D. | -2,1,0 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
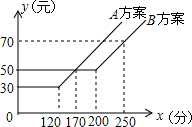 如图,某电信公司提供了A,B两种方案的移动通讯费用y(元)与通话时间x(分)之间的关系,下列四种结论:
如图,某电信公司提供了A,B两种方案的移动通讯费用y(元)与通话时间x(分)之间的关系,下列四种结论:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
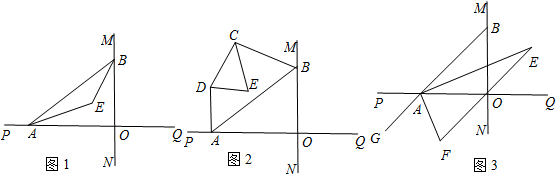
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
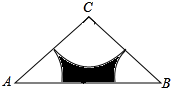 如图,在△ABC中,∠C=120°,CA=CB=6,分别以A,B,C为圆心,以3为半径画弧,三条弧与AB所围成的阴影部分的周长是3π+6$\sqrt{3}$-6.
如图,在△ABC中,∠C=120°,CA=CB=6,分别以A,B,C为圆心,以3为半径画弧,三条弧与AB所围成的阴影部分的周长是3π+6$\sqrt{3}$-6.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com