
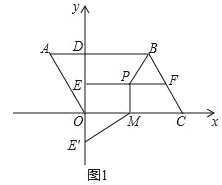
【题目】如图1,已知平行四边形ABCO,以点O为原点,OC所在的直线为x轴,建立直角坐标系,AB交y轴于点D,AD=2,OC=6,∠A=60°,线段EF所在的直线为OD的垂直平分线,点P为线段EF上的动点,PM⊥x轴于点M点,点E与E′关于x轴对称,连接BP、E′M.
(1)请直接写出点A的坐标为_____,点B的坐标为_____;
(2)当BP+PM+ME′的长度最小时,请直接写出此时点P的坐标为_____;
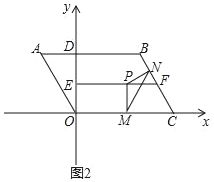
(3)如图2,点N为线段BC上的动点且CM=CN,连接MN,是否存在点P,使△PMN为等腰三角形?若存在,请求出所有满足要求的EP的值;若不存在,请说明理由.
【答案】(1)(﹣2,2![]() ),(4,2
),(4,2![]() );(2)(2,
);(2)(2,![]() );(3)EP的值为3或6﹣
);(3)EP的值为3或6﹣![]() 或5.
或5.
【解析】
(1)由30°直角三角形的性质求出OD的长,再由平行四边形的性质求出BD的长即可解决问题;
(2)首先证明四边形OPME′是平行四边形,可得OP=EM,因为PM是定值,推出PB+ME′=OP+PB的值最小时,BP+PM+ME′的长度最小;
(3)分三种情形画出图形分别求解即可解决问题.
(1)如图1中,
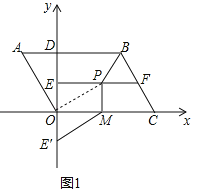
在Rt△ADO中,∵∠A=60°,∴∠AOD=30°.∵AD=2,∴OD =2![]() ,∴A(﹣2,2
,∴A(﹣2,2![]() ),
),
∵四边形ABCO是平行四边形,∴AB=OC=6,∴DB=6﹣2=4,∴B(4,2![]() );
);
(2)如图1中,连接OP.
∵EF垂直平分线段OD,PM⊥OC,∴∠PEO=∠EOM=∠PMO=90°,∴四边形OMPE是矩形,∴PM=OE=![]() .
.
∵OE=OE′,∴PM=OE′,PM∥OE′,∴四边形OPME′是平行四边形,∴OP=EM,
∵PM是定值,∴PB+ME′=OP+PB的值最小时,BP+PM+ME′的长度最小,∴当O、P、B共线时,BP+PM+ME′的长度最小.
∵直线OB的解析式为y=![]() x,∴P(2,
x,∴P(2,![]() ).
).
故答案为:(2,![]() ).
).
(3)如图2中,当PM=PN=![]() 时,
时,
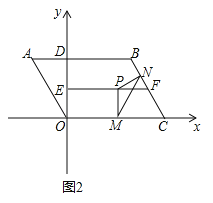
∵AOCB是平行四边形,∴∠MCN=∠A=60°.∵MC=CN,∴△MNC是等边三角形,∴∠CMN=∠CNM=60°.
∵PM⊥OC,∴∠PMN=∠PNM=30°,∴∠PNF=30°+60°=90°,
∵∠PFN=∠BCO=60°,∴∠NPF=30°,NF=1,∴PF=2NF=2,
∵EF=![]() =5,∴PE=5﹣2=3.
=5,∴PE=5﹣2=3.
如图3中,当PM=MN时,
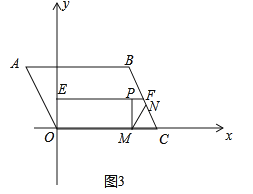
∵PM=MN=CM=![]() ,∴EP=OM=6﹣
,∴EP=OM=6﹣![]() .
.
如图4中,当点P与F重合时,NP=NM,此时PE=EF=5.
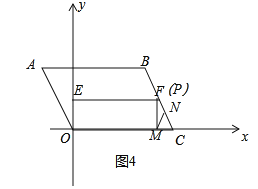
综上所述:满足条件的EP的值为3或6﹣![]() 或5.
或5.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y= ![]() x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P是直线AC下方抛物线上的动点.
x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P是直线AC下方抛物线上的动点. 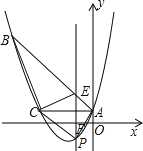
(1)求抛物线的解析式;
(2)过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F,当四边形AECP的面积最大时,求点P的坐标;
(3)当点P为抛物线的顶点时,在直线AC上是否存在点Q,使得以C、P、Q为顶点的三角形与△ABC相似,若存在,求出点Q的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司为一工厂代销一种建筑材料(这里的代销是指厂家先免费提供货源,待货物售出后再进行结算,未售出的由厂家负责处理).当每吨售价为260元时,月销售量为45吨.该经销店为提高经营利润,准备采取降价的方式进行促销.经市场调查发现:当每吨售价每下降10元时,月销售量就会增加7.5吨.综合考虑各种因素,每售出一吨建筑材料共需支付厂家及其它费用100元.设每吨材料售价为x(元),该经销店的月利润为y(元).
(1)当每吨售价是240元时,计算此时的月销售量;
(2)求出y与x的函数关系式(不要求写出x的取值范围);
(3)该经销店要获得最大月利润,售价应定为每吨多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△BAD是由△BEC在平面内绕点B旋转60°而得,且AB⊥BC,BE=CE,连接DE. 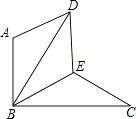
(1)求证:△BDE≌△BCE;
(2)试判断四边形ABED的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰Rt△ABC中,∠BAC=90°,AB=AC=10,等腰直角三角形ADE绕着点A旋转,∠DAE=90°,AD=AE=6,连接BD、CD、CE,点M、P、N分别为DE、DC、BC的中点,连接MP、PN、MN,则△PMN的面积最大值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图像与反比例函数y= ![]() 的图像交于点A﹙﹣2,﹣5﹚C﹙5,n﹚,交y轴于点B,交x轴于点D.
的图像交于点A﹙﹣2,﹣5﹚C﹙5,n﹚,交y轴于点B,交x轴于点D. 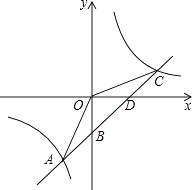
(1)求反比例函数y= ![]() 和一次函数y=kx+b的表达式;
和一次函数y=kx+b的表达式;
(2)连接OA,OC.求△AOC的面积.、
查看答案和解析>>
科目:初中数学 来源: 题型:
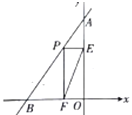
【题目】如图,直线AB的解析式为y=![]() x+4,与y轴交于点A,与x轴交于点B,点P为线段AB上的一个动点,作PE⊥y轴于点E,PF⊥x轴于点F,连接EF,则线段EF的最小值为_____.
x+4,与y轴交于点A,与x轴交于点B,点P为线段AB上的一个动点,作PE⊥y轴于点E,PF⊥x轴于点F,连接EF,则线段EF的最小值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,购买一种苹果,所付款金额y(元)与购买量x(千克)之间的函数图象由线段OA和射线AB组成,则一次购买5千克这种苹果比分五次购买1千克这种苹果可节省( )元.

A. 4 B. 5 C. 6 D. 7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,对角线AC与BD交于点O;在Rt△PMN中,∠MPN=90°.
(1)如图1,若点P与点O重合且PM⊥AD、PN⊥AB,分别交AD、AB于点E、F,请直接写出PE与PF的数量关系;
(2)将图1中的Rt△PMN绕点O顺时针旋转角度α(0°<α<45°).
①如图2,在旋转过程中(1)中的结论依然成立吗?若成立,请证明;若不成立,请说明理由;
②如图2,在旋转过程中,当∠DOM=15°时,连接EF,若正方形的边长为2,请直接写出线段EF的长;
③如图3,旋转后,若Rt△PMN的顶点P在线段OB上移动(不与点O、B重合),当BD=3BP时,猜想此时PE与PF的数量关系,并给出证明;当BD=mBP时,请直接写出PE与PF的数量关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com