
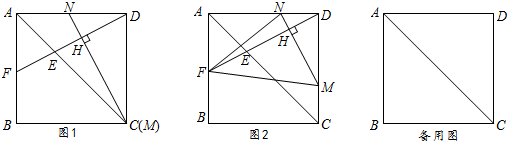
���� ��1�����ж���ADF�ա�DNC�����ɵõ����ۣ�
��2���ٵ���F��AB�е�ʱ���ɱ���ʽ$\frac{AE}{CE}=\frac{AF}{CD}$�����㼴�ɣ�
���ȱ�ʾ��AF��DN=CM=t��AN=DM=4-t���ٷ�����������㣮
��� ֤������1���ߡ�DNC+ADF=90�㣬��DNC+��DCN=90�㣬
���ADF=��DCN��
�ڡ�ADF�͡�DNC��
$\left\{\begin{array}{l}{��DAF=��CDN}\\{AD=CD}\\{��ADF=��DCN}\end{array}\right.$��
���ADF�ա�DNC��
��DF=MN��
��2���ٵ���F��AB�е�ʱ��
��AF=$\frac{1}{2}$AB=2��
�������֪��CM=t��AE=$\sqrt{2}$t��CE=4$\sqrt{2}$-$\sqrt{2}$t��
��AB��CD��
��$\frac{AE}{CE}=\frac{AF}{CD}$��
��$\frac{\sqrt{2}t}{4\sqrt{2}-\sqrt{2}t}=\frac{2}{4}$��
��t=$\frac{4}{3}$��
�ڡߡ�AEF�ס�CED��
��$\frac{AF}{CD}=\frac{AE}{CE}$��
��$\frac{AF}{4}=\frac{\sqrt{2}t}{4\sqrt{2}-\sqrt{2}t}$��
��AF=$\frac{4t}{4-t}$��
�ߡ�MND�ס�DFA��
��$\frac{ND}{AF}=\frac{DM}{AD}$��
��$\frac{ND}{\frac{4t}{4-t}}=\frac{4-t}{4}$��
��DN=CM=t��AN=DM=4-t��
�ߡ�MNF�ǵ��������Σ�
��FN=FM��
��MN��DF��
��FD��MN�Ĵ�ֱƽ���ߣ�
��DN=DM��
��t=4-t��
��t=2����ʱ��F���B�غϣ���
��FM=MNʱ����F��BC�ϣ���ͼ1��
�ߡ�NDM=��MCF��ND=MC��FM=MN��
���MFC�ա�NMD��
��FC=DM=4-t��
�ߡ�NDM�ס�DCF��
��$\frac{DN}{DM}=\frac{DC}{FC}$��
��$\frac{t}{4-t}=\frac{4}{4-t}$��
��t=4����ʱ��F��E���C�غϣ���M���D�غϣ������N�͵�A�غ�ʱ���������⣬��N���͵�A�غ�ʱ�����������⣬���ԣ���ȥ����
��FN=MNʱ����ͼ2��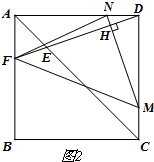
�ߡ�FAN=��NDM��AN=DM��FN=MN��
���FAN�ա�NDM��
��AF=DN��
��$\frac{4t}{4-t}$=t
��t=0�����������⣩��
������t=2ʱ����MNF�ǵ��������Σ�
���� �������ı����ۺ��⣬��Ҫ���������������ε����ʺ��ж���ȫ�������ε����ʺ��ж����߶εĴ�ֱƽ���ߵ��ж������ʣ��Ȿ��Ĺؼ������˶�ʱ���ʾ�߶Σ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 8 | B�� | 10 | C�� | 12 | D�� | 10��12 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��1���ⲻ��ʽ$\left\{\begin{array}{l}{2x+1��-3}\\{\frac{x+3}{5}��\frac{2x-5}{3}+1}\end{array}\right.$���Ѳ���ʽ��Ľ⼯�������ϱ�ʾ��
��1���ⲻ��ʽ$\left\{\begin{array}{l}{2x+1��-3}\\{\frac{x+3}{5}��\frac{2x-5}{3}+1}\end{array}\right.$���Ѳ���ʽ��Ľ⼯�������ϱ�ʾ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ����ƽ���ı���ABCD�У�AC��BD�ཻ�ڵ�O�������н��۲�һ���������ǣ�������
��ͼ����ƽ���ı���ABCD�У�AC��BD�ཻ�ڵ�O�������н��۲�һ���������ǣ�������| A�� | BO=DO | B�� | S��COD=S��AOD | C�� | ��BAD=��BCD | D�� | AC=BD |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
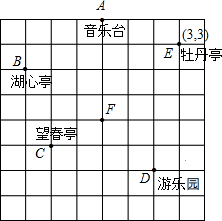 ���Ͱְ֡�������ĩ�������棬�ص��Һ�������ƽ��ֱ������ϵ�����˹��ľ�����ͼ����ͼ��ʾ����������������ͼ�б��ԭ���x�ᡢy�ᣮֻ֪��ĵ��������Ϊ��3��3���������������ƽ��ֱ������ϵ������ͼ�У��������������������ꣿ
���Ͱְ֡�������ĩ�������棬�ص��Һ�������ƽ��ֱ������ϵ�����˹��ľ�����ͼ����ͼ��ʾ����������������ͼ�б��ԭ���x�ᡢy�ᣮֻ֪��ĵ��������Ϊ��3��3���������������ƽ��ֱ������ϵ������ͼ�У��������������������ꣿ�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
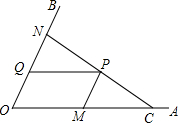 ��ͼ��CΪ��AOB�ı�OA��һ�㣬OC=6��NΪ��OB�����ڵ�O��һ���㣬P���߶�CN��һ�㣬����P�ֱ���PQ��OA��OB�ڵ� Q��PM��OB��OA�ڵ�M��
��ͼ��CΪ��AOB�ı�OA��һ�㣬OC=6��NΪ��OB�����ڵ�O��һ���㣬P���߶�CN��һ�㣬����P�ֱ���PQ��OA��OB�ڵ� Q��PM��OB��OA�ڵ�M���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
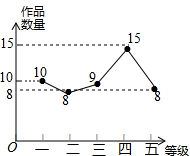 ijУ���ú��ٽ��пƼ�ʵ�������ѧ֮���ˣ�1����Ը����Ͻ��ġ��Ƽ���Ʒ��������������ͳ�ƣ�����������ͼ������ͳ��ͼ��
ijУ���ú��ٽ��пƼ�ʵ�������ѧ֮���ˣ�1����Ը����Ͻ��ġ��Ƽ���Ʒ��������������ͳ�ƣ�����������ͼ������ͳ��ͼ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0 | B�� | -$\frac{1}{2}$ | C�� | -2 | D�� | $\sqrt{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
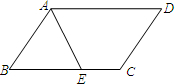 ��ͼ��?ABCD���ܳ�Ϊ16����BAD��ƽ����AE��CD�ڵ�E����BE=2����CE���ڣ�������
��ͼ��?ABCD���ܳ�Ϊ16����BAD��ƽ����AE��CD�ڵ�E����BE=2����CE���ڣ�������| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com