已知Rt△ABC的三个顶点A、B、C均在抛物线上y=x2,并且斜边AB平行于x轴,求这个直角三角形斜边上的高.
解:由题A,B,C均在抛物线y=x
2上,并且斜边AB平行于x轴,
知A、B两点关于y轴对称,记斜边AB交y轴于点D,
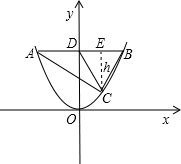
可设A(-

,b),B(

,b),C(a,a
2),D(0,b)
则因斜边上的高为h,
故:h=b-a
2,
∵△ABC是直角三角形,由其性质直角三角形斜边中线等于斜边一半,
∴得CD=

∴
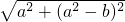
=

平方得:(b-a
2)=(a
2-b)
2
即h=(-h)
2
因h>0,得h=1,是个定值.
所以这个直角三角形斜边上的高为1.
分析:由抛物线表达式和三角形性质求出A、B、C各点坐标,就可以求出h的值.
点评:此题考查二次函数y=x
2图象的性质,直角三角形的性质,观察图形的能力,要找到各点坐标之间的关系,巧妙地代换未知量.


 ,b),B(
,b),B( ,b),C(a,a2),D(0,b)
,b),C(a,a2),D(0,b)
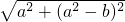 =
= 平方得:(b-a2)=(a2-b)2
平方得:(b-a2)=(a2-b)2

 名校课堂系列答案
名校课堂系列答案