
已知二次函数 :
:
(1) 证明:当m为整数时,抛物线 与x轴交点的横坐标均为整数;
与x轴交点的横坐标均为整数;
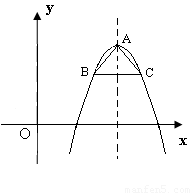
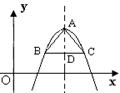
(2) 以抛物线 的顶点A为等腰Rt△的直角顶点,作该抛物线的内接等腰Rt△ABC(B、C两点在抛物线上),求Rt△ABC的面积(图中给出的是m取某一值时的示意图);
的顶点A为等腰Rt△的直角顶点,作该抛物线的内接等腰Rt△ABC(B、C两点在抛物线上),求Rt△ABC的面积(图中给出的是m取某一值时的示意图);
(3) 若抛物线 与直线y=7交点的横坐标均为整数,求整数m的值.
与直线y=7交点的横坐标均为整数,求整数m的值.
(1)证明:令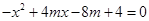 ,解得抛物线与
,解得抛物线与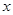 轴交点的横坐标x,
轴交点的横坐标x,
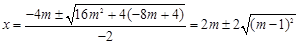 ,
,
∵m是整数,∴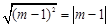 是整数,∴
是整数,∴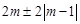 均为整数
均为整数
(2) 求得顶点A(2m,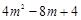 ),根据抛物线的轴对称性,所以BC平行x轴,
),根据抛物线的轴对称性,所以BC平行x轴,
作AD⊥BC,设B(a,b),则D在对称轴上,D(2m,b),
则BD=2m-a,(2m>a),
AD=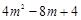 -b
-b
=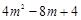
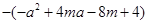 =(2m-a)2
=(2m-a)2
∵AD=BD, ∴(2m-a)2=(2m-a), 解得2m-a=1或2m-a=0(舍去)
∴S△ABC=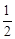 BCAD=
BCAD=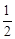 ×2BD×AD=1
×2BD×AD=1
(3)由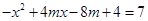 ,
,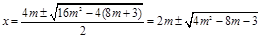 ,
,
当x为整数时,须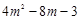 为完全平方数,设
为完全平方数,设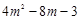
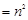 (n是整数)整理得:
(n是整数)整理得: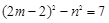 即
即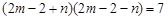
两个整数的积为7,∴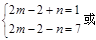 ~
~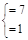 ~
~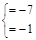 ~
~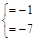
解得: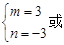
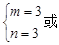
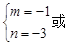
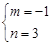 综上得: m=3或m=-1
综上得: m=3或m=-1
∴抛物线与直线y=7交点的横坐标均为整数时,m=3或m=-1.
【解析】(1)表示出横坐标,然后分析是整数;
(2)得出BC平行x轴、D在对称轴上是求三角形面积的关键;
(3)当x为整数时,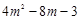 为完全平方数,然后根据两个整数的积=7求解。
为完全平方数,然后根据两个整数的积=7求解。


科目:初中数学 来源: 题型:
| A、y1≥y2 | B、y1>y2 | C、y1<y2 | D、y1≤y2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•莒南县二模)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:
(2013•莒南县二模)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:查看答案和解析>>
科目:初中数学 来源: 题型:
 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:①ac>0;②a-b+c<0;
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:①ac>0;②a-b+c<0;查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com