
小明和小方分别设计了一种求n边形的内角和(n-2)×180°(n为大于2的整数)的方案:
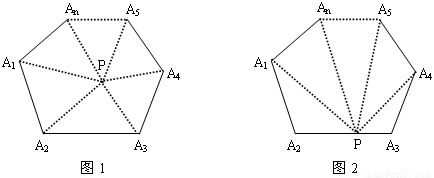
(1)小明是在n边形内取一点P,然后分别连结PA1、PA2、…、PAn(如图1);
(2)小红是在n边形的一边A1A2上任取一点P,然后分别连结PA4、PA5、…、PA1(如图2).
请你评判这两种方案是否可行?如果不行的话,请你说明理由;如果可行的话,请你沿着方案的设计思路把多边形的内角和求出来.
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:2012-2013学年河北省涉县七年级下学期期末考试数学试卷(带解析) 题型:解答题
小明和小方分别设计了一种求n边形的内角和(n-2)×180°(n为大于2的整数)的方案: 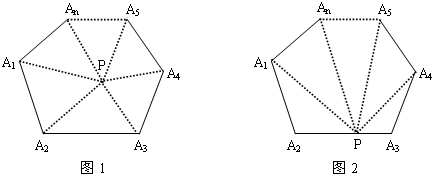
(1)小明是在n边形内取一点P,然后分别连结PA1、PA2、…、PAn(如图1);
(2)小红是在n边形的一边A1A2上任取一点P,然后分别连结PA4、PA5、…、PA1(如图2).
请你评判这两种方案是否可行?如果不行的话,请你说明理由;如果可行的话,请你沿着方案的设计思路把多边形的内角和求出来.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com