练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知AD为△ABC外角的平分线上的一点．求证：DB＋DC＞AB＋AC．

    答案：
    解析：

    　　证明：在BA边的延长线上取一点P．

    　　使AP＝AC　　又∠1＝∠2　　AD＝AD

    　　∴△ADP≌△ADC(SAS)

    　　∴DC＝DP

    　　在△DBP中

    　　DB＋PD＞PB

    　　∴DB＋PD＞AB＋AP

    　　即　　DB＋DC＞AB＋AC


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    已知，如图：Rt△ABC中，∠ABC=90°，AB=8，BC=10，D为△ABC外一点，连接AD，BD，过D作DH⊥AB，垂精英家教网足为H，交AC于E．
    （1）若△ABD是等边三角形，求DE的长为
     
    ；
    （2）若BD=AB，且tan∠HDB=
    34
    ，求DE的长为
     
    ．
    （根据2007年重庆中考题改编）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

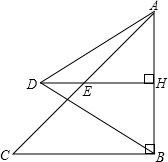    精英家教网已知，如图：△ABC是等腰直角三角形，∠ABC=90°，AB=10，D为△ABC外一点，连接AD、BD，过D作DH⊥AB，垂足为H，交AC于E．
    （1）若△ABD是等边三角形，求DE的长；
    （2）若BD=AB，且tan∠HDB=
    34
    ，求DE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    （2013•河池）如图（1），在Rt△ABC，∠ACB=90°，分别以AB、BC为一边向外作正方形ABFG、BCED，连结AD、CF，AD与CF交于点M．
    （1）求证：△ABD≌△FBC；
    （2）如图（2），已知AD=6，求四边形AFDC的面积；
    （3）在△ABC中，设BC=a，AC=b，AB=c，当∠ACB≠90°时，c2≠a2+b2．在任意△ABC中，c2=a2+b2+k．就a=3，b=2的情形，探究k的取值范围（只需写出你得到的结论即可）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

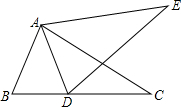    已知：如图，点D为△ABC的边BC上一点，且AB=AD，点E为△ABC外一点，连接AE、DE，使得∠ADE=∠B，∠CAE=∠BAD．
    求证：BC=DE．

    查看答案和解析>>

    科目：初中数学 来源：2013年初中毕业升学考试（广西河池卷）数学（解析版） 题型：解答题

    如图（1），在Rt△ABC, ∠ACB=90°,分别以AB、BC为一边向外作正方形ABFG、BCED，连结AD、CF，AD与CF交于点M。

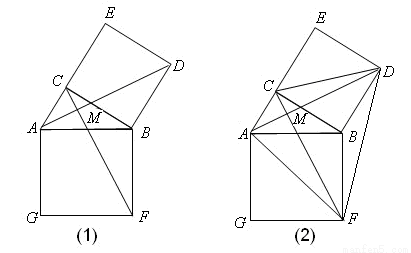
    （1）求证：△ABD≌△FBC；

    （2）如图（2），已知AD=6，求四边形AFDC的面积；

    （3）在△ABC中，设BC＝a，AC＝b，AB＝c，当∠ACB≠90°时，c2≠a2 ＋b2。在任意△ABC中，c2＝a2 ＋b2＋k。就a＝3，b＝2的情形，探究k的取值范围（只需写出你得到的结论即可）。

     

    查看答案和解析>>

    同步练习册答案