
【题目】抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
, ![]() ,与
,与![]() 轴交于
轴交于![]() .
.
(1)若![]() ,求抛物线的解析式,并写出抛物线的对称轴;
,求抛物线的解析式,并写出抛物线的对称轴;
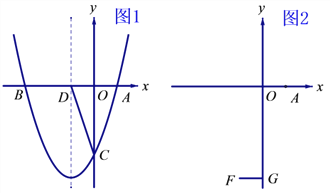
(2)如图1,在(1)的条件下,设抛物线的对称轴交轴于![]() ,在对称轴左侧的抛物线上有一点
,在对称轴左侧的抛物线上有一点![]() ,使
,使![]() ,求点
,求点![]() 的坐标;
的坐标;
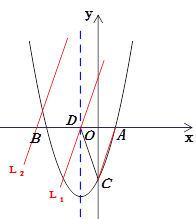
(3)如图2,设![]() ,
, ![]() 于
于![]() ,在线段
,在线段![]() 上是否存在点
上是否存在点![]() ,使
,使![]() ?若存在,求
?若存在,求![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
【答案】(1)抛物线的解析式为:y=x2+2x-3,对称轴为:x=-1;(2)点E坐标为(-4,5);(3)m的取值范围是:-4≤m≤4,且m≠0.
【解析】试题分析:(1)利用待定系数法即可得解析式,再根据抛物线对称轴公式即可得对称轴;
(2)先求出AC的解析式,然后求出过点D与AC平行的直线解析式,即可得到直线AC向上平移了6个单位长度,再根据![]() 可知点E为直线AC向上平移20个单位长度后与抛物线的交点,联立解析式解方程组即可得;
可知点E为直线AC向上平移20个单位长度后与抛物线的交点,联立解析式解方程组即可得;
(3)分m>0、m<0两种情况进行讨论即可得.
试题解析:(1)∵![]() 与
与![]() 轴交于
轴交于![]() ,
, ![]() ,m=-3,
,m=-3,
∴![]() ,解得
,解得![]() ,
,
∴抛物线的解析式为:y=x2+2x-3,
对称轴为:x=-1;
(2)∵点A(1,0),C(0,-3),
∴直线AC为y= 3x-3,
∴过点D(-1,0)且平行于AC的直线ll为:y= 3x+3,
∴直线AC向上平移6个单位得到直线l1,
∴将直线AC向上平移![]() 个单位得到直线l2:y=3x+17,
个单位得到直线l2:y=3x+17,
联立方程组, ![]() ,
,
解得, ![]() ,
, ![]() (不合题意,舍去),
(不合题意,舍去),
∴点E坐标为(-4,5);
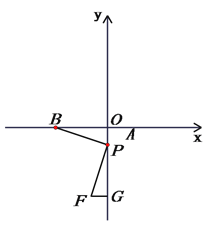
(3)设点P(0,y),
①当m<0时,如图所示,易证△POB~△FPG,得![]() ,
,
∴![]() ,
,
∴m=y2+4y=(y+2)2-4,
∵-4<y<0,
∴-4≤m<0;
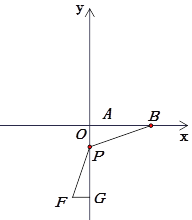
②当m>0时,如图所示,易证△POB~△FPG,得![]() ,
,
∴![]() ,
,
∴m= -y2 -4y= -(y+2)2+4,
∵-4<y<0,
∴0<m≤4,
综上所述,m的取值范围是:-4≤m≤4,且m≠0.


 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:初中数学 来源: 题型:
【题目】如图,在正方形![]() 中,
中,![]() ,
,![]() 为
为![]() 上一动点,
上一动点,![]() 交
交![]() 于
于![]() ,过
,过![]() 作
作![]() 交
交![]() 于
于![]() ,连接
,连接![]() ,过
,过![]() 作
作![]() 于
于![]() ,下列有四个结论:①
,下列有四个结论:①![]() ,②
,②![]() ,③
,③![]() ,④
,④![]() 的周长为定值,其中正确的结论有( ).
的周长为定值,其中正确的结论有( ).

A.①②③B.①②④C.①③④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A,B的坐标分别为(-1,0),(3,0),现同时将点A,B分别向上平移2个单位长度,再向右平移1个单位长度,得到A,B的对应点C,D,连接AC,BD,CD.
(1)直接写出点C,D的坐标,求出四边形ABDC的面积;
(2)在x轴上是否存在一点F,使得三角形DFC的面积是三角形DFB面积的2倍,若存在,请求出点F的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地电话拨号入网有两种收费方式,用户可以任选其一.
计时制:0.05元/分;
包月制:50元/月(限一部个人住宅电话上网).
此外,每一种上网方式都得加收通信费0.02元/分.
(1)某用户某月上网的时间为x小时,请你分别写出两种收费方式下该用户应该支付的费用.
(2)若某用户估计一个月内上网的时间为20小时,你认为采用哪种方式较为合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形 ABCD中AB= 3,点B在边CD上,且 CD=3DE. 将△ADE沿AE对折至△AFE,延长EF交边BC 于点G,连接AG,CF下列结论:①点G是BC的中点;②FG=FC;③![]() GAE=45;④GE=BG+DE.其中正确的是( )
GAE=45;④GE=BG+DE.其中正确的是( )

A. ①② B. ①③④ C. ②③ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,正方形ABCD,点P是直线BC上一个动点,连接PD交直线AB于点O,过点B作BE⊥PD于点E,连接AE.



(1)如图1,
①直接写出∠AED的度数;
②用等式表示线段AE、BE和DE之间的数量关系,并证明;
(2)当点P运动到图2和图3所示的位置时,请选择其中一种情况补全图形,并接写出线段AE、BE和DE之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解某校九年级男生的体能情况,体育老师随即抽取部分男生进行引体向上测试,并对成绩进行了统计,绘制成图1和图2尚不完整的统计图.
(1)本次抽测的男生有多少人?请你将条形统计图补充完整;
(2)本次抽测成绩的众数是 ;
(3)若规定引体向上5次以上(含5次)为体能达标,则该校350名九年级男生中,估计有多少人体能达标?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,O是坐标原点,一次函数y=kx+b的图象与x轴交于点A(﹣3,0),与y轴交于点B,且与正比例函数y=![]() x的图象的交点为C(m,4).
x的图象的交点为C(m,4).

(1)求一次函数y=kx+b的解析式;
(2)D是平面内一点,以O、C、D、B四点为顶点的四边形是平行四边形,直接写出点D的坐标.(不必写出推理过程).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com