
���� ��1���ɷ���������y=$\frac{k}{x}$��ͼ���ڶ������ޣ��õ�k��0�����ǵõ�һ�κ���Ϊy=kx+b��x���������С������A��D���ڵ�һ���ޣ��õ�����ʽ���ɵõ����ۣ�
��2����������õ�$\frac{3k+b}{k+b}=\frac{3}{4}$���������ε������ʽ�õ�S��OEF=$\frac{1}{2}$����-$\frac{b}{k}$����b=$\frac{27}{2}$������������k=-$\frac{1}{3}$��b=3�����ɵõ����ۣ�
��� 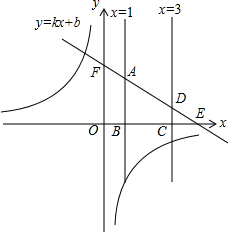 �⣺��1��֤�����߷���������y=$\frac{k}{x}$��ͼ���ڶ������ޣ�
�⣺��1��֤�����߷���������y=$\frac{k}{x}$��ͼ���ڶ������ޣ�
��k��0��
��һ�κ���Ϊy=kx+b��x���������С��
��A��D���ڵ�һ���ޣ�
��3k+b��0��
��b��-3k��
��2��������֪��$\frac{ED}{EA}=\frac{CD}{AB}$��
��$\frac{3k+b}{k+b}=\frac{3}{4}$ �٣�
��E��-$\frac{b}{k}$��0����F��0��b����
��S��OEF=$\frac{1}{2}$����-$\frac{b}{k}$����b=$\frac{27}{2}$ �ڣ�
�ɢ٢������������ã�k=-$\frac{1}{3}$��b=3��
�����һ�κ����Ľ���ʽΪy=-$\frac{1}{3}$x+3��
��-$\frac{1}{3x}$=-$\frac{1}{3}$x+3��x1=$\frac{9-\sqrt{85}}{2}$��x2=$\frac{9+\sqrt{85}}{2}$��
��ֱ��y=kx+b�뷴��������y=$\frac{k}{x}$�Ľ�������ĺ�������$\frac{9-\sqrt{85}}{2}$��$\frac{9+\sqrt{85}}{2}$��
���ʽ$\frac{k}{x}$��kx+b�Ľ⼯Ϊ$\frac{9-\sqrt{85}}{2}$��x��0��x��$\frac{9+\sqrt{85}}{2}$��
���� ���⿼���˷�����������һ�κ��������ʣ������Ľ���ʽ�������������ʽ��Ӧ�ã��������շ�����������һ�κ����������ǽ���Ĺؼ���


 �������Ӳ�ϵ�д�
�������Ӳ�ϵ�д� ���ɿ��õ�Ԫ����AB��ϵ�д�
���ɿ��õ�Ԫ����AB��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
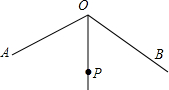 ��ͼ����AOB=120�㣬OPƽ�֡�AOB����OP=2������M��N�ֱ���OA��OB�ϣ��ҡ�PMNΪ�ȱ������Σ����������������ġ�PMN�У�������
��ͼ����AOB=120�㣬OPƽ�֡�AOB����OP=2������M��N�ֱ���OA��OB�ϣ��ҡ�PMNΪ�ȱ������Σ����������������ġ�PMN�У�������| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 3������ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ�����Ϊ24��������ABCD�У���һ��С������EFGH������E��F��G�ֱ���AB��BC��FD�ϣ���BF=$\frac{\sqrt{6}}{2}$����С�����ε��ܳ�Ϊ��������
��ͼ�����Ϊ24��������ABCD�У���һ��С������EFGH������E��F��G�ֱ���AB��BC��FD�ϣ���BF=$\frac{\sqrt{6}}{2}$����С�����ε��ܳ�Ϊ��������| A�� | $\frac{5\sqrt{6}}{8}$ | B�� | $\frac{5\sqrt{6}}{6}$ | C�� | $\frac{5\sqrt{6}}{2}$ | D�� | $\frac{10\sqrt{6}}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
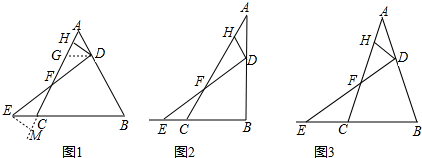
 ��ͼ��ʾ����ABC�У�E��F�ֱ��DZ�AB��AC�ϵĵ㣬������$\frac{AE}{EB}$=$\frac{AF}{FC}$=$\frac{1}{2}$�����AEF��
��ͼ��ʾ����ABC�У�E��F�ֱ��DZ�AB��AC�ϵĵ㣬������$\frac{AE}{EB}$=$\frac{AF}{FC}$=$\frac{1}{2}$�����AEF���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com