
【题目】如图(1),![]() ,
,![]() ,
,![]() ,
,![]() .点
.点![]() 在线段
在线段![]() 上以
上以![]() 的速度由点
的速度由点![]() 向点
向点![]() 运动,同时,点
运动,同时,点![]() 在线段
在线段![]() 上由点
上由点![]() 向点
向点![]() 运动,它们运动的时间为
运动,它们运动的时间为![]()
(1)若点![]() 的运动速度与点
的运动速度与点![]() 的运动速度相等,当
的运动速度相等,当![]() 时,判断线段
时,判断线段![]() 与
与![]() 满足的关系,并说明理由;
满足的关系,并说明理由;
(2)如图(2),将图(1)中的“![]() ,
,![]() ”为改“
”为改“![]() ”,其它条件不变.设点
”,其它条件不变.设点![]() 的运动速度为
的运动速度为![]() ,是否存在实数
,是否存在实数![]() ,使得
,使得![]() 与
与![]() 全等?若存在,求出相应的
全等?若存在,求出相应的![]() 、
、![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
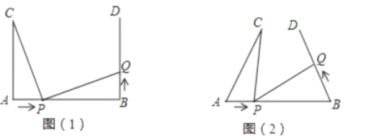
【答案】(1)PC=PQ且PC⊥PQ,证明见解析;(2)存在,①x=2,t=1,②x=3,t=2,详情见解析;
【解析】
(1)利用SAS证得△ACP≌△BPQ,可得PC=PQ,得出∠ACP=∠BPQ,进一步得出∠APC+∠BPQ=∠APC+∠ACP=90°得出PC⊥PQ;
(2)由△ACP≌△BPQ,分两种情况:①AC=BP,AP=BQ,②AC=BQ,AP=BP,建立方程组求得答案即可;
证明:(1)PC=PQ且PC⊥PQ;理由如下:
∵AC⊥AB,BD⊥AB,
∴∠A=∠B=90°,
当![]() 时,AP=BQ=2,
时,AP=BQ=2,
∴BP=AB-AP=8-2=6,
∴BP=AC=6,
在△ACP和△BPQ中,
 ,
,
∴△ACP≌△BPQ,
∴PC=PQ,
∴∠C=∠QPB,
∵∠APC+∠C=90°,
∴∠APC+∠QPB=90°,
即PC=PQ且PC⊥PQ;
(2)存在x的值,使得△ACP与△BPQ全等,
①若△ACP≌△BPQ,
则AC=BP,AP=BQ,
可得:6=8-2t,2t=xt,
解得:x=2,t=1;
②若△ACP≌△BQP,
则AC=BQ,AP=BP,
可得:6=xt,2t=8-2t,
解得:x=3,t=2.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:
【题目】张师傅驾车从甲地去乙地,途中在加油站加了一次油,加油时,车载电脑显示还能行驶50千米.假设加油前、后汽车都以100千米/小时的速度匀速行驶,已知油箱中剩余油量y(升)与行驶时间t(小时)之间的关系如图所示.

(1)求张师傅加油前油箱剩余油量y(升)与行驶时间t(小时)之间的关系式;
(2)求出a的值;
(3)求张师傅途中加油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2002年8月在北京召开的国际数学家大会会标取材于我国古代数学家赵爽的《勾股圆方图》,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形(如图所示).如果大正方形的面积是13,小正方形的面积是1,直角三角形的较短直角边为a,较长直角边为b,那么(a+b)2的值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
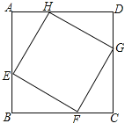
【题目】已知:正方形ABCD中,点E、F、G、H分别在AB、BC、CD、DA上,且AE=BF=CG=DH,
(1)四边形EFGH是正方形吗?为什么?
(2)若正方形ABCD的边长为4cm,且AE=BF=CG=DH=3cm,请求出四边形EFGH的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知四边形ABCD中,AB∥DC,连接BD,BE平分∠ABD,BE⊥AD,∠EBC和∠DCB的角平分线相交于点F,若∠ADC=110°,则∠F的度数为( )
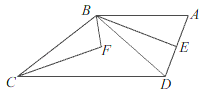
A. 115° B. 110° C. 105° D. 100°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABD≌△CDB,且AB,CD是对应边.下面四个结论中不正确的是( )

A. △ABD和△CDB的面积相等B. △ABD和△CDB的周长相等
C. ∠A+∠ABD=∠C+∠CBDD. AD∥BC,且AD=BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】节日里,兄弟两人在60米的跑道上进行短距离比赛,两人从出发点同时起跑,哥哥到达终点时,弟弟离终点还差12米.
(1)若哥哥的速度为10米/秒,
①求弟弟的速度;
②如果两人重新开始比赛,哥哥从起点向后退10米,兄弟同时起跑,两人能否同时到达终点?若能,请求出两人到达终点的时间;若不能,请说明谁先到达终点.
(2)若哥哥的速度为m米/秒,
①弟弟的速度为________米/秒(用含m的代数式表示);
②如果两人想同时到达终点,哥哥应向后退多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A,B的坐标分别为(1,0),(2,0).若二次函数y=x2+(a﹣3)x+3的图象与线段AB只有一个交点,则a的取值范围是_______________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
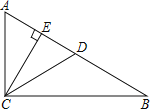
【题目】在直角三角形ABC中,∠ACB=90°,D、E是边AB上两点,且CE所在直线垂直平分线段AD,CD平分∠BCE,BC=2![]() ,则AB=_____.
,则AB=_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com