
【题目】定义:有一个角是其邻角一半的圆内接四边形叫做圆内倍角四边形.
(1)如图1,四边形ABCD内接于⊙O,∠DCB﹣∠ADC=∠A,求证:四边形ABCD为圆内接倍角四边形;
(2)在(1)的条件下,⊙O半径为5.
①若AD为直径,且sinA=![]() ,求BC的长;
,求BC的长;
②若四边形ABCD中有一个角为60°,且BC=CD,则四边形ABCD的面积是 ;
(3)在(1)的条件下,记AB=a,BC=b,CD=c,AD=d,求证:d2﹣b2=ab+cd.

【答案】(1)见解析;(2)①BC=6,②![]() 或
或![]() ;(3)见解析
;(3)见解析
【解析】
(1)先判断出∠ADC=180°﹣2∠A.进而判断出∠ABC=2∠A,即可得出结论;
(2)①先用锐角三角函数求出BD,进而得出AB,由(1)得出∠ADB=∠BDC,即可得出结论;
②分两种情况:利用面积和差即可得出结论;
(3)先得出BE=BC=b,DE=DA=b,进而得出CE=d﹣c,再判断出△EBC∽△EDA,即可得出结论.
(1)设∠A=α,则∠DCB=180°﹣α.
∵∠DCB﹣∠ADC=∠A,∴∠ADC=∠DCB﹣∠A=180°﹣α﹣α=180°﹣2α,∴∠ABC=180°﹣∠ADC=2α=2∠A,∴四边形ABCD是⊙O内接倍角四边形;
(2)①连接BD.
∵AD是⊙O的直径,∴∠ABD=90°.在Rt△ABD中,AD=2×5=10,sin∠A=![]() ,∴BD=8,根据勾股定理得:AB=6,设∠A=α,∴∠ADB=90°﹣α.
,∴BD=8,根据勾股定理得:AB=6,设∠A=α,∴∠ADB=90°﹣α.
由(1)知,∠ADC=180°﹣2α,∴∠BDC=90°﹣α,∴∠ADB=∠BDC,∴BC=AB=6;

②若∠ADC=60°时.
∵四边形ABCD是圆内接倍角四边形,∴∠BCD=120°或∠BAD=30°.
Ⅰ、当∠BCD=120°时,如图3,连接OA,OB,OC,OD.
∵BC=CD,∴∠BOC=∠COD,∴∠OCD=∠OCB=![]() ∠BCD=60°,∴∠CDO=60°,∴AD是⊙O的直径,(为了说明AD是直径,点O没有画在AD上)
∠BCD=60°,∴∠CDO=60°,∴AD是⊙O的直径,(为了说明AD是直径,点O没有画在AD上)
∴∠ADC+∠BCD=180°,∴BC∥AD,∴AB=CD.
∵BC=CD,∴AB=BC=CD,∴△OAB,△BOC,△COD是全等的等边三角形,∴S四边形ABCD=3S△AOB=3×![]() ×52=
×52=![]() .
.
Ⅱ、当∠BAD=30°时,如图4,连接OA,OB,OC,OD.
∵四边形ABCD是圆内接四边形,∴∠BCD=180°﹣∠BAD=150°.
∵BC=CD,∴∠BOC=∠COD,∴∠BCO=∠DCO=![]() ∠BCD=75°,∴∠BOC=∠DOC=30°,∴∠OBA=45°,∴∠AOB=90°.
∠BCD=75°,∴∠BOC=∠DOC=30°,∴∠OBA=45°,∴∠AOB=90°.
连接AC,∴∠DAC=![]() ∠BAD=15°.
∠BAD=15°.
∵∠ADO=∠OAB﹣∠BAD=15°,∴∠DAC=∠ADO,∴OD∥AC,∴S△OAD=S△OCD.
过点C作CH⊥OB于H.
在Rt△OCH中,CH=![]() OC=
OC=![]() ,∴S四边形ABCD=S△COD+S△BOC+S△AOB﹣S△AOD=S△BOC+S△AOB=
,∴S四边形ABCD=S△COD+S△BOC+S△AOB﹣S△AOD=S△BOC+S△AOB=![]() ×5+
×5+![]() ×5×5=
×5×5=![]() .
.
故答案为:![]() 或
或![]() ;
;

(3)延长DC,AB交于点E.
∵四边形ABCD是⊙O的内接四边形,∴∠BCE=∠A=![]() ∠ABC.
∠ABC.
∵∠ABC=∠BCE+∠A,∴∠E=∠BCE=∠A,∴BE=BC=b,DE=DA=b,∴CE=d﹣c.
∵∠BCE=∠A,∠E=∠E,∴△EBC∽△EDA,∴![]() ,∴
,∴![]() ,∴d2﹣b2=ab+cd.
,∴d2﹣b2=ab+cd.


科目:初中数学 来源: 题型:
【题目】为弘扬中华传统文化,黔南州近期举办了中小学生“国学经典大赛”,比赛项目为:A.唐诗;B.宋词;C.论语;D.三字经.比赛形式为两人对抗赛,即把四种比赛项目写在4张完全相同的卡片上,比赛时,比赛的两人从中随机抽取1张卡片作为自己的比赛项目(不放回,且每人只能抽取一次)比赛时,小红和小明分到一组.(1)小明先抽取,那么小明抽到唐诗的概率是多少?
(2)小红擅长唐诗,小红想:“小明先抽取,我后抽取”抽到唐诗的概率是不同的,且小明抽到唐诗的概率更大,若小红后抽取,小红抽中唐诗的概率是多少?小红的想法对吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
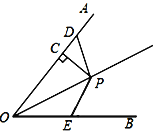
【题目】如图,P为∠AOB的平分线上一点,PC⊥OA于点C,D为OA上一点,E为OB上一点,∠ODP=180°-∠OEP.
(1)求证:PD=PE.
(2)若OC=6,求OD+OE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段EF的长为( )
,将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段EF的长为( )

A.![]() B.
B.![]() C.4D.
C.4D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
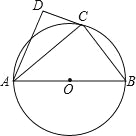
【题目】如图,⊙O的直径为AB,点C在圆周上(异于A,B),AD⊥CD.
(1)若BC=3,AB=5,求AC的值;
(2)若AC是∠DAB的平分线,求证:直线CD是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小强骑车从家到学校要经过一段先上坡后下坡的路,在这段路上小强骑车的距离s(千米)与骑车的时间t(分钟)之间的函数关系如图所示,请根据图中信息回答下列问题:

(1)小强去学校时下坡路长 千米;
(2)小强下坡的速度为 千米/分钟;
(3)若小强回家时按原路返回,且上坡的速度不变,下坡的速度也不变,那么回家骑车走这段路的时间是 分钟.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】反比例函数![]() 和一次函数y=k2x+b的图象交于点M(3,﹣
和一次函数y=k2x+b的图象交于点M(3,﹣![]() )和点N(﹣1,2),则k1=_____,k2=____,一次函数的图象交x轴于点_____.
)和点N(﹣1,2),则k1=_____,k2=____,一次函数的图象交x轴于点_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为满足市场需求,新生活超市在端午节前夕购进价格为3元/个的某品牌粽子,根据市场预测,该品牌粽子每个售价4元时,每天能出售500个,并且售价每上涨0.1元,其销售量将减少10个,为了维护消费者利益,物价部门规定,该品牌粽子售价不能超过进价的200%,请你利用所学知识帮助超市给该品牌粽子定价,使超市每天的销售利润为800元.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com