
【题目】如图所示,在矩形ABCD中,对角线AC,BD相交于点O,∠BOC=120°,AC=6,求: 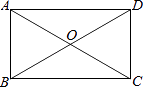
(1)AB的长;
(2)矩形ABCD的面积.
【答案】
(1)解:∵四边形ABCD是矩形,
∴OB=OC,∠ABC=90°,
又∵∠BOC=120°,
∴∠OBC=∠OCB=30°,
∴AB= ![]() AC=
AC= ![]() ×6=3
×6=3
(2)解:∵AB2+BC2=AC2,
∴BC= ![]() =3
=3 ![]() ,
,
∴矩形ABCD的面积=AB×BC=3×3 ![]() =9
=9 ![]()
【解析】(1)根据OB=OC,∠ABC=90°,以及∠BOC=120°,可得出∠OBC=∠OCB=30°,进而得到AB= ![]() AC=3;(2)根据勾股定理即可得出BC=
AC=3;(2)根据勾股定理即可得出BC= ![]() =3
=3 ![]() ,进而得出矩形ABCD的面积.
,进而得出矩形ABCD的面积.
【考点精析】认真审题,首先需要了解含30度角的直角三角形(在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半),还要掌握勾股定理的概念(直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2)的相关知识才是答题的关键.


科目:初中数学 来源: 题型:
【题目】先阅读下面的材料,再回答后面的问题:
计算:10÷(![]() -
-![]() +
+![]() ).
).
解法一:原式=10÷![]() -10÷
-10÷![]() +10÷
+10÷![]() =10×2-10×3+10×6=50;
=10×2-10×3+10×6=50;
解法二:原式=10÷(![]() -
-![]() +
+![]() )=10÷
)=10÷![]() =10×3=30;
=10×3=30;
解法三:原式的倒数为(![]() -
-![]() +
+![]() )÷10
)÷10
=(![]() -
-![]() +
+![]() )×
)×![]() =
=![]() ×
×![]() -
-![]() ×
×![]() +
+![]() ×
×![]() =
=![]()
故原式=30.
(1)上面得到的结果不同,肯定有错误的解法,你认为解法 是错误的。
(2)请选择一种上述的正确方法解决下面的问题:
计算:(![]() )÷(
)÷(![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠![]() 是锐角,∠
是锐角,∠![]() 是钝角,且∠
是钝角,且∠![]() +∠
+∠![]() =180°,那么下列结论正确的是( )
=180°,那么下列结论正确的是( )
A. ∠![]() 的补角和∠
的补角和∠![]() 的补角相等 B. ∠
的补角相等 B. ∠![]() 的余角和∠
的余角和∠![]() 的补角相等
的补角相等
C. ∠![]() 的余角和∠
的余角和∠![]() 的补角互余 D. ∠
的补角互余 D. ∠![]() 的余角和∠
的余角和∠![]() 的补角互补
的补角互补
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将点A先向下平移3个单位长度,再向右平移4个单位长度,得到点A'(-3,-6),则点A的坐标为( )
A. (-7,3)B. (6,-10)C. (-7,-3)D. (-1,-10)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请你从下列条件:①AB=CD,②AD=BC,③AB∥CD,④AD∥BC中任选两个,使它们能判定四边形ABCD是平行四边形.共有________种情况符合要求.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com