
【题目】如图1,将一个边长为a厘米的正方形纸片剪去两个小矩形,得到图案,如图2所示,再将剪下的两个小矩形拼成一个新的矩形,如图3所示:
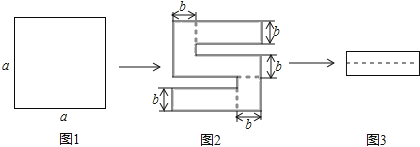
(1)列式表示新矩形的周长为______厘米(化到最简形式)
(2)如果正方形纸片的边长为8厘米,剪去的小矩形的宽为1厘米,那么所得图形的周长为______厘米.
科目:初中数学 来源: 题型:
【题目】小明和同桌小聪在课后复习时,对练习册“目标与评定”中的一道思考题,进行了认真地探索.
(思考题)如图,一架2.5米长的梯子AB斜靠在竖直的墙AC上,这时B到墙C的距离为0.7米,如果梯子的顶端沿墙下滑0.4米,那么点B将向外移动多少米?
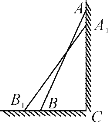
(1)请你将小明对“思考题”的解答补充完整:
解:设点B将向外移动x米,即BB1=x,
则A1B1=2.5,在Rt△A1B1C中,由B1C2+A1C2=A1B12,
得方程___________________,解方程,得x1=____,x2=______________,∴点B将向外移动____米.
(2)解完“思考题”后,小聪提出了如下两个问题:
(问题一)在“思考题”中,将“下滑0.4米”改为“下滑0.9米”,那么该题的答案会是0.9米吗?为什么?
(问题二)在“思考题”中,梯子的顶端从A处沿墙AC下滑的距离与点B向外移动的距离,有可能相等吗?为什么?
请你解答小聪提出的这两个问题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知O为直线AB上的一点,射线OA表示正北方向,∠COE=90°,射线OF平分∠AOE.
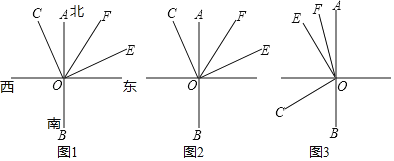
(1)如图1,若∠AOE=70°,则∠COF的度数是 ;
(2)若将∠COE绕点O旋转至图2的位置,试判断∠COF和∠BOE之间的数量关系,并证明你的证明;
(3)若将∠COE绕点O旋转至图3的位置,直接写出2∠COF+∠BOE的度数是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】司机小王沿东西大街跑出租车,约定向东为正,向西为负,某天自![]() 地出发到收工时,行走记录为(单位:千米):+8、-9、+7、-12、+5、-10、+17、-13.
地出发到收工时,行走记录为(单位:千米):+8、-9、+7、-12、+5、-10、+17、-13.
回答下列问题:
(1)收工时小王在![]() 地的哪边?距
地的哪边?距![]() 地多少千米?
地多少千米?
(2)若每千米耗油0.2升,问从![]() 地出发到收工时,共耗油多少升?
地出发到收工时,共耗油多少升?
(3)在工作过程中,小王最远离![]() 地多远?在
地多远?在![]() 地哪边?
地哪边?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有理数a,b,c在数轴上的位置如图所示,且|a|=|b|.
![]()
(1)用“>”“<”或“=”填空:
b______0,a+b______0,a-c______0,b-c______0;
(2)化简:|c-a|-|c-b|+|a+b|.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知菱形A1B1C1D1的边长为2,且∠A1B1C1=60°,对角线A1C1,B1D1相较于点O,以点O为坐标原点,分别以OA1,OB1所在直线为x轴、y轴,建立如图所示的直角坐标系,以B1D1为对角线作菱形B1C2D1A2 ,使得∠B1A2D1=60°;再以A2C2为对角线作菱形A2B2C2D2,使得∠A2B2C2=60°;再以B2D2为对角线作菱形B2C3D2A3,使得∠B2A3D2=60°…,按此规律继续作下去,在x轴的正半轴上得到点A1,A2,A3,…,An,则点A2018的坐标为______.
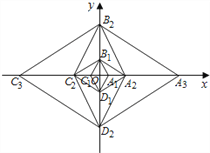
查看答案和解析>>
科目:初中数学 来源: 题型:
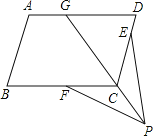
【题目】如图,点G、E、F分别在平行四边形ABCD的边AD、DC和BC上,DG=DC,CE=CF,点P是射线GC上一点,连接FP,EP.
求证:FP=EP.
查看答案和解析>>
科目:初中数学 来源: 题型:
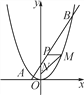
【题目】如图,已知一条直线过点(0,4),且与抛物线y=![]() x2交于A,B两点,其中点A的横坐标是-2.
x2交于A,B两点,其中点A的横坐标是-2.
(1)求这条直线的解析式及点B的坐标;
(2)在x轴上是否存在点C,使得△ABC是直角三角形?若存在,求出点C的坐标,若不存在,请说明理由;
(3)过线段AB上一点P,作PM∥x轴,交抛物线于点M,点M在第一象限,点N(0,1),当点M的横坐标为何值时,MN+3MP的长度最大?最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】蜜蜂是自然界神奇的“建筑师“,它能用最少的材料造成最牢固的建筑物“蜂窝“,观察下列的“蜂窝图
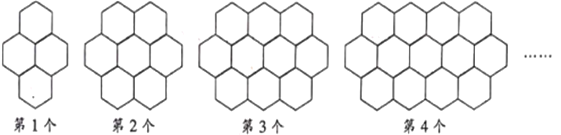
(1)若“![]() ”中每条边看成1个建筑单位,则第1个图形中共有19个建筑单位,第2个图案中共有_____个建筑单位;第3个图案中共有_____个建筑单位.
”中每条边看成1个建筑单位,则第1个图形中共有19个建筑单位,第2个图案中共有_____个建筑单位;第3个图案中共有_____个建筑单位.
(2)第n个图案中共有多少个建筑单位.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com