
��2013���Ĵ��㰲10�֣���ͼ����ƽ��ֱ������ϵxOy�У�������y=ax2+bx+c����A��B��C���㣬��֪��A����3��0����B��0��3����C��1��0����

��1����������ߵĽ���ʽ��
��2����P��ֱ��AB�Ϸ�����������һ���㣬�������A��B�غϣ�������P��x��Ĵ��ߣ�����ΪF����ֱ��AB�ڵ�E����PD��AB�ڵ�D��
�ٶ���P��ʲôλ��ʱ����PDE���ܳ���������ʱP������ꣻ
������PA����APΪ����ͼʾһ���������APMN�����ŵ�P���˶��������εĴ�С��λ��Ҳ��֮�ı䣮������M��Nǡ�����������߶Գ�����ʱ�������Ӧ��P������꣮������������ţ�
�⣺��1����������y=ax2+bx+c������A����3��0����B��0��3����C��1��0����
��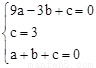 �����
�����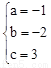 ��
��
�������ߵĽ���ʽΪy=��x2��2x+3��
��2���١�A����3��0����B��0��3������OA=OB=3�����AOB�ǵ���ֱ�������Ρ����BAO=45�㡣
��PF��x�ᣬ���AEF=90�㩁45��=45�㡣
�֡�PD��AB�����PDE�ǵ���ֱ�������Ρ���PDԽ��PDE���ܳ�Խ��
��ֱ��AB�Ľ���ʽΪy=x+3��
����ABƽ�е�ֱ�߽���ʽΪy=x+m��
����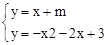 ������y�ã�x2+3x+m��3=0��
������y�ã�x2+3x+m��3=0��
����=32��4��1����m��3��=0����m=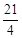 ʱ��ֱ����������ֻ��һ�����㣬PD���
ʱ��ֱ����������ֻ��һ�����㣬PD���
��ʱx=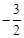 ��y=
��y=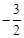 +
+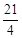 =
=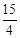 ��
��
���P��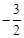 ��
��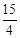 ��ʱ����PDE���ܳ����
��ʱ����PDE���ܳ����
��������y=��x2��2x+3�ĶԳ���Ϊֱ�� ��
��
��i����ͼ1����M�ڶԳ�����ʱ������P��PQ�ͶԳ�����Q��

��������APMN�У�AP=PM����APM=90�㣬
���APF+��FPM=90�㣬��QPM+��FPM=90�㡣
���APF=��QPM��
���ڡ�APF�͡�MPQ�У�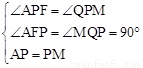 �����APF�ա�MPQ��AAS������PF=PQ��
�����APF�ա�MPQ��AAS������PF=PQ��
���P�ĺ�����Ϊn��n��0������PQ=��1��n����PF=��1��n�����P������Ϊ��n����1��n����
�ߵ�P��������y=��x2��2x+3�ϣ��ੁn2��2n+3=��1��n�������ã�n2+n��4=0��
���n1= ����ȥ����n2=
����ȥ����n2= ����1��n=��1��
����1��n=��1�� =
= ��
��
���P�������� ��
�� ����
����
��ii����ͼ2����N�ڶԳ�����ʱ���������߶Գ�����x�ύ�ڵ�Q��

�ߡ�PAF+��FPA=90�㣬��PAF+��QAN=90�㣬���FPA=��QAN��
�֡ߡ�PFA=��AQN=90�㣬PA=AN�����APF�ա�NAQ��
��PF=AQ��
���P����ΪP��x����x2��2x+3����
����x2��2x+3=��1������3��=2��
���x=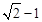 ���������⣬��ȥ����x=
���������⣬��ȥ����x=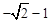 ��
��
���P������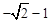 ��2����
��2����
����������������Mǡ�����������߶Գ�����ʱ����P����Ϊ�� ��
�� ����������Nǡ�����������߶Գ�����ʱ����P������Ϊ��
����������Nǡ�����������߶Գ�����ʱ����P������Ϊ��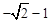 ��2����
��2����
����������1���ѵ�A��B��C��������������߽���ʽ�����ô���ϵ��������κ�������ʽ��ɡ�
��2���ٸ��ݵ�A��B���������OA=OB���Ӷ��õ���AOB�ǵ���ֱ�������Σ����ݵ���ֱ�������ε����ʿɵá�BAO=45�㣬Ȼ�������PED�ǵ���ֱ�������Σ����ݵ���ֱ�������ε����ʣ�PDԽ��PDE���ܳ�������жϳ�����ֱ��ABƽ�е�ֱ����������ֻ��һ������ʱ��PD��������ֱ��AB�Ľ���ʽΪy=x+3������ABƽ�е�ֱ�߽���ʽΪy=x+m���������߽���ʽ��������y���õ�����x��һԪ���η��̣����ø����б�ʽ��=0��ʽ���m��ֵ�������x��y��ֵ���Ӷ��õ���P�����ꡣ
����ȷ���������ߵĶԳ��ᣬȻ��i���ֵ�M�ڶԳ�����ʱ������P��PQ�ͶԳ�����Q������ͬ�ǵ������������APF=��QPM�������á��ǽDZߡ�֤����APF�͡�MPQȫ�ȣ�����ȫ�������ζ�Ӧ����ȿɵ�PF=PQ�����P�ĺ�����Ϊn����ʾ��PQ�ij�����PF��Ȼ����������߽���ʽ���㼴�ɵý⣻��ii����N�ڶԳ�����ʱ��ͬ�������APF�͡�ANQȫ�ȣ�����ȫ�������ζ�Ӧ����ȿɵ�PF=AQ�����ݵ�A�����������P�������꣬�ٴ��������߽���ʽ��������꣬���ɵõ���P�����ꡣ
���㣺���κ����ۺ��⣬���������⣬�����ϵ�������뷽�̵Ĺ�ϵ������ֱ�������ε��ж������ʣ�һԪ���η��̸����б�ʽ����һԪ���η��̣������ε����ʣ�ȫ�������ε��ж������ʣ�����˼���Ӧ�á�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2013����б�ҵ��ѧ���ԣ��Ĵ��㰲������ѧ�������棩 ���ͣ������
��2013���Ĵ��㰲9�֣���ͼ���ڡ�ABC�У�AB=AC����ABΪֱ������Բ��0����BC�ڵ�D������AD������D��DE��AC������Ϊ��E����AB���ӳ����ڵ�F��

��1����֤��EF�ǡ�0�����ߣ�
��2�������O�İ뾶Ϊ5��sin��ADE= ����BF�ij���
����BF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2013����б�ҵ��ѧ���ԣ��Ĵ��㰲������ѧ�������棩 ���ͣ������
��2013���Ĵ��㰲8�֣��Ű�«ɽ����7.0�������ijУʦ������һЩ����ֱ��������ֽƬ����ÿ��ֽƬ�м���һ����Բ������ߣ��ĸ�������С���ѣ���֪��ͼ��������Ϊ4�ĵ���ֱ��������ABC��Ҫ������İ�Բ��ֱ���ڡ�ABC�ı��ϣ��Ұ�Բ�Ļ����ABC�������������У����������в�ͬ������ʾ��ͼ���������Ӧ��Բ�İ뾶������������ţ���
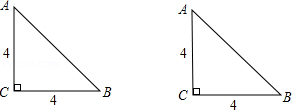
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2013����б�ҵ��ѧ���ԣ��Ĵ��㰲������ѧ�������棩 ���ͣ������
��2013���Ĵ��㰲8�֣���ͼ���㰲�з���ָ�Ӳ�����������һ����400�ף���8�ף���ˮ�µ��½�Ϊ45��ķ����̣������Ϊ����ABCD������ӹ̣���������֤������ָ�Ӳ�ר�����ƶ��ļӹ̷����ǣ���ˮ��������ʯ���мӹ̣���ʹ�ϵӿ�2�ף��ӹ̺�ˮ��EF���±�i=1��2��
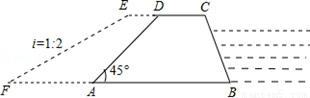
��1����ӹ̺�ӵ����ӵĿ���AF�ij���
��2��������������Ҫ��ʯ���������ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2013����б�ҵ��ѧ���ԣ��Ĵ��㰲������ѧ�������棩 ���ͣ������
��2013���Ĵ��㰲8�֣�ij�̳��O�ʽ�12.8��Ԫ��һ���Թ����յ����ʵ繲30̨�������г���Ҫ����Щ�յ����ʵ����ȫ�����ۣ�ȫ�����ۺ���������1.5��Ԫ�����пյ����ʵ�Ľ��ۺ��ۼۼ�����
|
|
�յ� |
�ʵ� |
|
���ۣ�Ԫ/̨�� |
5400 |
3500 |
|
�ۼۣ�Ԫ/̨�� |
6100 |
3900 |
���̳��ƻ������յ�x̨���յ��Ͳʵ�ȫ�����ۺ��̳���õ�����ΪyԪ��
��1����д��y��x�ĺ�����ϵʽ��
��2���̳����ļ��ֽ��������ɹ�ѡ��
��3��ѡ�����ֽ����������̳����������������Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2013����б�ҵ��ѧ���ԣ��Ĵ��㰲������ѧ�������棩 ���ͣ������
��2013���Ĵ��㰲6�֣�6��5���ǡ����绷���ա����㰲��ijУ�����ˡ������������ݽ�������������������ͬѧ�ijɼ�����ѧ���ijɼ��ֳ�A��B��C��D�ĸ��ȼ������Ƴ������µ�����ͳ��ͼ������ͼ����ͼ1��ͼ2����
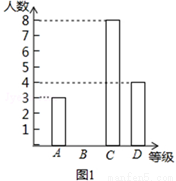
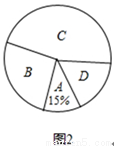
��1����ȫ����ͳ��ͼ��
��2��ѧУ�����ӱ��α����л��A��B��ѧ���и�ѡ��һ��ȥ�μ�����ѧ�������ݽ���������֪A����������2����B����Ů����3 ���������á��б�����������ͼ�����ķ��������ѡ��λͬѧǡ����һ��������һ��Ů���ĸ��ʣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com