
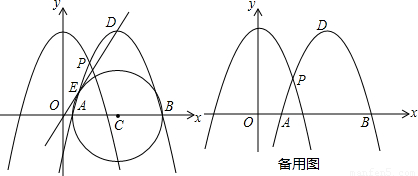
 ,则k=OC=
,则k=OC= ;
; ,-
,- k2+4),再利用待定系数法求出直线OD的解析式为y=
k2+4),再利用待定系数法求出直线OD的解析式为y= x,然后将点P的坐标代入y=
x,然后将点P的坐标代入y= x,即可求出k的值.
x,即可求出k的值. (2)①如图,连接CE,CD.
(2)①如图,连接CE,CD. ,
, ;
; ,能够使得点O、P、D三点恰好在同一条直线上.理由如下:
,能够使得点O、P、D三点恰好在同一条直线上.理由如下: ,x2=0(不合题意舍去),
,x2=0(不合题意舍去), 时,y=-
时,y=- k2+4,
k2+4, ,-
,- k2+4).
k2+4). ,
, x,
x, ,-
,- k2+4)在直线y=
k2+4)在直线y= x上,得-
x上,得- k2+4=
k2+4= •
• ,
, (负值舍去),
(负值舍去), 时,O、P、D三点在同一条直线上.
时,O、P、D三点在同一条直线上. ,-
,- k2+4)代入直线OD的解析式,建立关于k的方程外,还可以利用相似三角形对应边成比例列式求解.
k2+4)代入直线OD的解析式,建立关于k的方程外,还可以利用相似三角形对应边成比例列式求解. 

科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
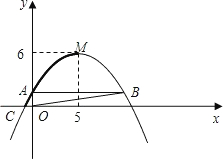 物线图象的一部分,如图中的粗线所示)在平移过程中所扫过的面积.
物线图象的一部分,如图中的粗线所示)在平移过程中所扫过的面积.查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•衡阳)如图所示,已知抛物线的顶点为坐标原点O,矩形ABCD的顶点A,D在抛物线上,且AD平行x轴,交y轴于点F,AB的中点E在x轴上,B点的坐标为(2,1),点P(a,b)在抛物线上运动.(点P异于点O)
(2012•衡阳)如图所示,已知抛物线的顶点为坐标原点O,矩形ABCD的顶点A,D在抛物线上,且AD平行x轴,交y轴于点F,AB的中点E在x轴上,B点的坐标为(2,1),点P(a,b)在抛物线上运动.(点P异于点O)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com