
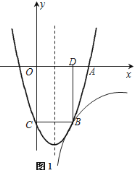
【题目】如图![]() ,二次函数
,二次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,过点
,过点![]() 作
作![]() 轴,交抛物线于点
轴,交抛物线于点![]() ,并过点
,并过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() .抛物线
.抛物线![]() 和反比例函数
和反比例函数![]() 的图象都经过点
的图象都经过点![]() ,四边形
,四边形![]() 的面积是
的面积是![]() .
.
![]() 求反比例函数、二次函数的解析式及抛物线的对称轴;
求反比例函数、二次函数的解析式及抛物线的对称轴;
![]() 如图
如图![]() ,点
,点![]() 从
从![]() 点出发以每秒
点出发以每秒![]() 个单位的速度沿线段
个单位的速度沿线段![]() 向
向![]() 点运动,点
点运动,点![]() 从
从![]() 点出发以相同的速度沿线段img src="http://thumb.zyjl.cn/questionBank/Upload/2019/05/12/08/1a8f9afd/SYS201905120854095644903087_ST/SYS201905120854095644903087_ST.023.png" width="24" height="19" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />向
点出发以相同的速度沿线段img src="http://thumb.zyjl.cn/questionBank/Upload/2019/05/12/08/1a8f9afd/SYS201905120854095644903087_ST/SYS201905120854095644903087_ST.023.png" width="24" height="19" style="-aw-left-pos:0pt; -aw-rel-hpos:column; -aw-rel-vpos:paragraph; -aw-top-pos:0pt; -aw-wrap-type:inline" />向![]() 点运动,其中一个动点到达端点时,另一个也随之停止运动.设运动时间为
点运动,其中一个动点到达端点时,另一个也随之停止运动.设运动时间为![]() 秒.
秒.
①当![]() 为何值时,四边形
为何值时,四边形![]() 为等腰梯形;
为等腰梯形;
②设![]() 与对称轴的交点为
与对称轴的交点为![]() ,过
,过![]() 点作
点作![]() 轴的平行线交
轴的平行线交![]() 于点
于点![]() ,设四边形
,设四边形![]() 的面积为
的面积为![]() ,求面积
,求面积![]() 关于时间
关于时间![]() 的函数解析式,并指出
的函数解析式,并指出![]() 的取值范围;当
的取值范围;当![]() 为何值时,
为何值时,![]() 有最大值或最小值.
有最大值或最小值.

【答案】![]()
![]() ,
,![]() ①当
①当![]() 秒时,四边形
秒时,四边形![]() 为等腰梯形②当
为等腰梯形②当![]() 秒时,面积
秒时,面积![]() 有最小值
有最小值![]() .
.
【解析】
(1)根据反比例函数的比例系数k的几何意义可求出k,从而可求出点B的坐标,然后运用待定系数法就可求出二次函数的解析式,由此可求出对称轴方程;
(2)①过点P作PE⊥OA,垂足为E,如图2,易证BC∥OA,要使四边形ABPQ为等腰梯形,只需PQ=AB,只需QE=AD=1,由此即可求出t的值;②如图2,易证△MFP≌△MGQ,则有MF=MG,从而可求出S△BPN(用t表示),然后只需求出S四边形ABPQ,并运用割补法就可得到S关于t的函数解析式,然后只需利用该函数的增减性就可解决问题.
![]() 如图
如图![]() ,
,
∵四边形![]() 的面积是
的面积是![]()
,
∴![]() ,
,
∴反比例函数的解析式为![]() .
.
∵反比例函数![]() 的图象经过点
的图象经过点![]() ,
,
∴![]() ,
,
解得![]() .
.
∴![]() .
.
将点![]() ,
,![]() 代入
代入![]() ,得
,得
![]()
解得:![]() ,
,
∴二次函数的解析式![]() .
.
则抛物线的对称轴为![]() ;
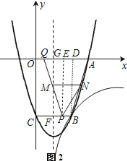
;![]() ①由题意可知:
①由题意可知:![]() .
.
∵点![]() ,点
,点![]() 的纵坐标相等,
的纵坐标相等,
∴![]() .
.
过点![]() 作
作![]() ,垂足为
,垂足为![]() ,如图
,如图![]() .
.
要使四边形![]() 为等腰梯形,只需
为等腰梯形,只需![]() .
.
即![]() .
.
又![]() ,
,
∴![]() .
.
解得![]() ,
,
∴当![]() 秒时,四边形
秒时,四边形![]() 为等腰梯形.
为等腰梯形.
②设对称轴与![]() 、
、![]() 轴的交点分别为
轴的交点分别为![]() 、
、![]() ,如图
,如图![]() .
.
∵对称轴![]() 是线段
是线段![]() 的垂直平分线,
的垂直平分线,
∴![]() .
.
又∵![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
在![]() 和
和![]() 中,
中,
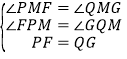
∴![]() ,
,
∴![]() ,
,
∴![]()
![]()
![]() .
.
∵![]()
![]()
![]() ,
,
∴![]()
![]() .
.
∵![]() ,
,![]() ,
,
∴点![]() 运动到点
运动到点![]() 时停止运动,需要
时停止运动,需要![]() 秒,
秒,
∴![]() .
.
∵![]() ,
,
∴当![]() 秒时,面积
秒时,面积![]() 有最小值
有最小值![]() .
.


 小题狂做系列答案
小题狂做系列答案科目:初中数学 来源: 题型:
【题目】甲乙两位同学用围棋子做游戏.如图所示,现轮到黑棋下子,黑棋下一子后白棋再下一子,使黑棋的![]() 个棋子组成轴对称图形,白棋的
个棋子组成轴对称图形,白棋的![]() 个棋子也成轴对称图形.则下列下子方法不正确的是( ),
个棋子也成轴对称图形.则下列下子方法不正确的是( ),![]() .
.

A. 黑(3,7);白(5,3) B. 黑(4,7);白(6,2)
C. 黑(2,7);白(5,3) D. 黑(3,7);白(2,6)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为24的等边三角形ABC中,M是高CH所在直线上的一个动点,连结MB,将线段BM绕点B逆时针旋转60°得到BN,连结HN.则在点M运动过程中,线段HN长度的最小值是( )

A. 12B. 6C. 3D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题探究:如图①,在四边形ABCD中,AB∥CD,E是BC的中点,AE是∠BAD的平分线,则线段AB,AD,DC之间的等量关系为 ;
(2)方法迁移:如图②,在四边形ABCD中,AB∥CD,AF与DC的延长线交于点F,E是BC的中点,AE是∠BAF的平分线,试探究线段AB,AF,CF之间的等量关系,并证明你的结论;
(3)联想拓展:如图③,AB∥CF,E是BC的中点,点D在线段AE上,∠EDF=∠BAE,试探究线段AB,DF,CF之间的数量关系,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着近几年我市私家车日越增多,超速行驶成为引发交通事故的主要原因之一.某中学数学活动小组为开展“文明驾驶、关爱家人、关爱他人”的活动,设计了如下检测公路上行驶的汽车速度的实验:先在公路旁边选取一点![]() ,在笔直的车道
,在笔直的车道![]() 上确定点
上确定点![]() ,使
,使![]() 和
和![]() 垂直,测得
垂直,测得![]() 的长等于
的长等于![]() 米,在
米,在![]() 上的同侧取点
上的同侧取点![]() 、
、![]() ,使
,使![]() ,
,![]() .
.

![]() 求
求![]() 、
、![]() 之间的路程(保留根号);
之间的路程(保留根号);
![]() 已知本路段对校车限速为
已知本路段对校车限速为![]() 米/秒若测得某校车从
米/秒若测得某校车从![]() 到
到![]() 用了
用了![]() 秒,这辆校车是否超速?请说明理由.
秒,这辆校车是否超速?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系的原点![]() 是正方形
是正方形![]() 的中心,顶点
的中心,顶点![]() ,
,![]() 的坐标分别为
的坐标分别为![]() 、
、![]() ,把正方形
,把正方形![]() 绕原点
绕原点![]() 逆时针旋转
逆时针旋转![]() 得到正方形
得到正方形![]() ,则正方形
,则正方形![]() 与正方形
与正方形![]() 重叠部分形成的正八边形的边长为( )
重叠部分形成的正八边形的边长为( )

A. ![]()
B. ![]()
C. ![]()
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】课上老师呈现一个问题:

下面提供三种思路:
思路一:过点F作MN∥CD(如图甲);
思路二:过P作PN∥EF,交AB于点N;
思路三:过O作ON∥FG,交CD于点N.
解答下列问题:

(1)根据思路一(图甲),可求得∠EFG的度数为 ;
(2)根据思路二、三分别在图乙和图丙中作出符合要求的辅助线;
(3)请你从思路二、思路三中任选其中一种,写出求∠EFG度数的解答过程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com